Ο Μεσαίωνας, ή αλλιώς οι Σκοτεινοί Χρόνοι, καλύπτει ένα μεγάλο χρονικό φάσμα της Ιστορίας, από την Αρχαιότητα έως την Αναγέννηση (476 μ.Χ.- 1492 μ.Χ.). Στα 1000 περίπου χρόνια Μεσαιωνικής Ιστορίας, κύριο χαρακτηριστικό είναι η στροφή προς τον συντηρητισμό, αλλά και η επιβολή της θεοκρατίας.
Παρόλο λοιπόν που ο μυστικισμός και η παπική εξουσία κυριαρχούσαν, μια νέα τάξη πραγμάτων δημιουργήθηκε. Καινούρια φύλα λαών εμφανίζονται για πρώτη φορά στον δυτικό κόσμο, όπως οι Ούννοι, οι Σάξονες και βέβαια οι Βίκινγκς. Νέες πρακτικές εφαρμόστηκαν στη γεωργία και η πολιτική σκηνή αναδιαρθρώθηκε. Ωστόσο, η κοινωνική και πνευματική ανάπτυξη που γνώρισε ο Ύστερος Μεσαίωνας, δεν στάθηκαν αρκετές για να αλλάξει την πεποίθηση των περισσότερων ότι οι άνθρωποι που ζούσαν τότε ήταν οπισθοδρομικοί και αγνώμονες.
Ορίστε, λοιπόν, οι 15 επικρατέστεροι μύθοι για τους Σκοτεινούς Χρόνους:
1. Η Γη είναι επίπεδη. Ήδη από τον Γαλιλαίο είχε ξεκινήσει η αμφισβήτηση της πίστης ότι η Γη δεν είναι επίπεδη και γυρίζει γύρω από τον Ήλιο και τον άξονα της. Το ίδιο πίστευαν και οι άνθρωποι του Μεσαίωνα, ωστόσο αργότερα για να αποδείξουν πόσο οπισθοδρομική ήταν η περίοδος αυτή, επικράτησε η άποψη που κυκλοφορούσε τον 19ο αιώνα: ότι οι Μεσαιωνικοί άνθρωποι ήταν σίγουροι ότι η Γη είναι επίπεδη.
2. Το δικαίωμα της «Πρώτης Νύχτας» ήταν υπαρκτό. Η primaenoctisή αλλιώς παρθενοφθορία εμφανίστηκε αρχικά σαν νομικός όρος στο Βυζάντιο τον 12ο αιώνα και ήταν σχετικό με το δικαίωμα γάμου των γυναικών. Αργότερα, αναπτύχθηκε ο αστικός μύθος ότι κατά τον Μεσαίωνα οι τοπικοί άρχοντες είχαν το δικαίωμα της «πρώτης νύχτας», με τις παρθένες συζύγους ζευγαριών που μόλις είχαν παντρευτεί. Η φήμη αυτή διαδόθηκε αρκετά στην Γαλλία του 19ου αιώνα, ωστόσο μετέπειτα ιστορικοί δηλώνουν ότι αναφορές περί παρθενοφθορίας δεν υπάρχουν.
3. Οι Βίκινγκς φορούσαν κράνη με κέρατα. Ο άγριος λαός από την Σκανδιναβία, με τους Ρούνους για γραφή και με πλούσια μυθολογία με θεούς όπως ο Όντιν, ο Λόκι και ο Θωρ, ποτέ δεν φόρεσαν κερασφόρα κράνη. Οι ικανότατοι πολεμιστές που πίστευαν στην αιώνια ζωή της Βαλχάλα πολεμούσαν με τσεκούρια, σφυριά κι άλλα λιγότερο εκλεπτυσμένα όπλα. Η ασπίδα ήταν απαραίτητη- όχι όμως και το κράνος, καθώς θα τους καθυστερούσε και θα τους περιόριζε την ορατότητά τους. Οι Βίκινγκς έχουν περάσει στην ιστορία σαν άγριος λαός με ανοιχτά χρώματα και χαρακτηριστικά κράνη με κέρατα στο κεφάλι, επειδή έτσι τους φαντάζονταν οι Σκανδιναβοί καλλιτέχνες του 19ου αιώνα.
4. Μηχανές βασανιστηρίων κατασκευάστηκαν τον Μεσαίωνα. Σαφώς και κατά τον Μεσαίωνα επινοήθηκαν νέα εργαλεία και τρόποι βασανισμού, όμως όχι ότι όλες οι τρομαχτικές και απίστευτα σκληρές μηχανές βασανιστηρίων ανακαλύφθηκαν τότε. Κατασκευές που πρόσφεραν αργό και σαδιστικό θάνατο, όπως το «αχλάδι του πνιγμού» (chokepear/pearofanguish), ή «καμπίνα του θανάτου» (ironmaiden), εμφανίζονται αρκετά χρόνια μετά το 1492 μ.Χ.
5. Προστριβές πάνω σε αδιάφορα θέματα, όπως το πόσοι άγγελοι βρίσκονται πάνω από ένα φωτοστέφανο. Μετέπειτα διανοούμενοι, στην προσπάθεια τους να αποδείξουν πόσο ντροπιαστική ήταν η υπερβολική επιμονή των ανθρώπων του Μεσαίωνα στην θρησκεία, αναφέρουν ότι πολλές φορές διαφωνούσαν για τελείως ασήμαντα θέματα. Μία από τις διαφωνίες τους φαίνεται να ήταν στον ακριβή αριθμό των αγγέλων που βρίσκονται και χορεύουν πάνω από τα κεφάλια θεολογικών φιγούρων. Πάλι, βέβαια, ιστορικοί τονίζουν ότι τέτοιες αναφορές είναι ανύπαρκτες.
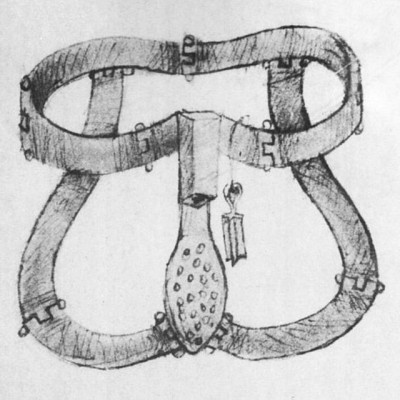
6. Ζώνες που εμποδίζουν τις γυναίκες από σεξουαλική συνεύρεση. Ο Μεσαίωνας καλύπτει και την περίοδο των Σταυροφοριών και άλλων μεγάλων, βέβαια, επιδρομών. Έτσι λοιπόν, ένας αστικός μύθος αναφέρει ότι οι άρχοντες, όταν έφευγαν από την πατρίδα τους για επιδρομές, ανάγκαζαν τις γυναίκες του φορούν μία μεταλλική ζώνη, με καρφάκια στην ευαίσθητη περιοχή τους, ώστε να μην μπορούν να ικανοποιηθούν σεξουαλικά, μέχρι την επιστροφή τους. Οι ζώνες αυτές υπήρχαν, ποτέ δεν χρησιμοποιήθηκαν, παρά μόνο αργότερα τον 19ο αιώνα που η στροφή προς τα περίεργα σαδιστικά και μη αντικείμενα του Μεσαίωνα ήταν αρκετά έντονη.
7. Το νερό δεν ήταν πόσιμο κι έτσι στον Μεσαίωνα έπιναν κρασί και μπύρα. Άλλος ένας μύθος. Η αλήθεια είναι ότι το νερό ήταν μολυσμένο κι έτσι αρκετοί απέφευγαν να το πιουν. Αρκετές βέβαια ήταν και οι πηγές καθαρού νερού, αλλά μόνο οι προύχοντες είχαν πρόσβαση και ορισμένοι αγρότες στην εξοχή. Επίσης, πολλοί συνήθιζαν να αραιώνουν το κρασί με νερό.
8. Η προσωπική υγιεινή των ανθρώπων στο Μεσαίωνα ήταν άθλια και οι ίδιοι ήταν συνέχεια βρόμικοι. Προφανώς και κατά τον Μεσαίωνα οι άνθρωποι έκαναν μπάνιο και προσπαθούσαν να είναι καθαροί. Χτένες και άλλα είδη προσωπικής υγιεινής ήταν εξίσου γνωστά. Πάντως το σίγουρο είναι ότι δεν έμεναν άλουστοι για να διατηρήσουν την περίτεχνη κόμμωσή τους, όπως αρκετές κυρίες συνήθιζαν τον 19ο αιώνα.
9.Το κάστρο Νόισβανσταϊν χτίστηκε τον Μεσαίωνα. Την εποχή του Μεσαίωνα αναπτύχθηκε ιδιαίτερα η γοτθική τέχνη. Το κάστρο Νόισβονσταϊν, ενώ έχει μείνει στην ιστορία ως ένα από τα καλύτερα μεσαιωνικά κάστρα, στην πραγματικότητα ακολουθεί τα βασικά χαρακτηριστικά του ρομαντισμού και απέχει πολύ από την ιδέα ενός μεσαιωνικού κάστρου-φρουρίου. Επίσης, η κατασκευή του ξεκίνησε το 1865 από το Λουδοβίκο Β΄ της Βαυαρίας ως χώρος ανάπαυσης και φόρος τιμής στον Ριχάρδο Βάγκνερ.
10. Οι τομάτες ήταν δηλητηριώδεις. Το ζουμερό αυτό κόκκινο σποροφυτό, ιδιαίτερα γνωστό στους ιθαγενείς της Λατινικής Αμερικής, προέρχεται από το Περού και δεν ήταν ακόμη γνωστό στη Μεσαιωνική Ευρώπη. Μόλις τον 16ο αιώνα έγινε ευρέως γνωστό στο μεγαλύτερο τμήμα της Ευρώπης, όταν και έγινε η εισαγωγή του προϊόντος από την Νότια Αμερική.
11. Ο προσδόκιμο ζωής ήταν κάτω από 30 έτη. Είναι γνωστό ότι κατά τον Μεσαίωνα το προσδόκιμο ζωής ήταν τρεις δεκαετίες. Όμως αυτό δεν σημαίνει ότι μετά τα τριάντα οι άνθρωποι πέθαιναν ή ότι ήταν ήδη μεσήλικες. Πολλοί ξεπέρασαν τα 30 χρόνια και έζησαν έως τα 70. Επιπλέον, η τρίτη ηλικία θεωρούταν τα 50 έτη.
12. Στον Μεσαίωνα δεν χρησιμοποιούσαν μαχαιροπίρουνα. Συνήθως οι άνθρωποι στον Μεσαίωνα γευμάτισαν με τα χέρια. Βέβαια, δεν έτρωγαν πάντα και μόνο με τα χέρια. Ενίοτε χρησιμοποιούσαν μαχαίρια και κουτάλια, σκεύη αρκετά διαδεδομένα κατά τη μεσαιωνική περίοδο. Το πιρούνι, από την άλλη, ήταν ήδη γνωστό από το 6ο αιώνα στο Βυζάντιο, ενώ ο ιταλικός Μεσαίωνας το έμαθε τον 11ο αιώνα.
13. Στους Σκοτεινούς Χρόνους οι άνθρωποι ποτέ δεν ταξίδευαν. Αρκετές αναφορές αποδεικνύουν ότι οι άνθρωποι κατά τον Μεσαίωνα ταξίδευαν. Ήταν αρκετά συνηθισμένο να μετακινούνται στην ενδοχώρα, ακόμη κι έξω από τα σύνορα. Ακόμη, πολύ συχνά τοπικοί άρχοντες επισκέπτονταν εκκλησίες και μοναστήρια που βρίσκονταν σε άλλες επαρχίες. Έτσι λοιπόν, η ιδέα ότι ένας άνθρωπος του Μεσαίωνα γεννιόταν, μεγάλωνε και πέθαινε στο χωριό του είναι μια γενίκευση στα όρια του μύθου.
14. Οι γυναίκες δεν είχαν δικαιώματα. Η άποψη ότι οι γυναίκες ήταν υποχείρια των αντρών τους και αντικείμενα διακοσμητικής θηλυκότητας δεν ισχύει. Οι γυναίκες λοιπόν ήταν σε θέση να κληρονομήσουν, να αγοράσουν και να πουλήσουν μια ιδιοκτησία καθώς επίσης είχαν το δικαίωμα να ανοίξουν μία δική τους επιχείρηση.
15. Όλοι οι άνθρωποι του Μεσαίωνα ήταν υπερβολικά θρησκόληπτοι. Αυτός ο μύθος δεν απέχει πολύ από την πραγματικότητα. Όντως ισχύει ότι οι άνθρωποι ήταν παραπάνω του φυσιολογικού θεοσεβούμενου και αφοσιωμένοι στην θρησκεία. Άλλωστε όλος ο Μεσαίωνας διακατέχεται από μια θεοκρατική επιβολή. Πάντα, όμως, υπάρχει η εξαίρεση στον κανόνα. Κληρικοί αναφέρουν ότι πολλοί άνθρωποι είχαν μια διαφορετική άποψη για τον καθολικισμό, αρκετοί δεν ήταν τόσο αφοσιωμένοι, ενώ και πολλοί άρχοντες είχαν διατηρήσει τις δικές τους θρησκευτικές πεποιθήσεις. Άλλωστε, πριν από τον Χριστιανισμό, ο Παγανισμός καθώς κι άλλες ειδωλολατρικές θρησκείες είχαν θέσει πολύ βαθιά τα θεμέλιά τους.
________
Πηγή: medievalists.net , mixanitouxronou.gr