Το θεωρούμενο ως «Nόμπελ» των Μαθηματικών Βραβείο Abel 2023 απονεμήθηκε στον 75χρονο Luis A. Caffarelli
Οι εξισώσεις είναι εργαλεία που χρησιμοποιούν οι επιστήμονες για να προβλέψουν τη συμπεριφορά του φυσικού κόσμου. Τα περισσότερα φυσικά φαινόμενα όπως, κύματα διαφόρων ειδών, ροή ρευστών, διάδοση θερμότητας, διάχυση κ.ά, μπορούν να εκφραστούν ως «Μερικές Διαφορικές Εξισώσεις (ΜΔΕ)», ένας τύπος εξίσωσεων με περισσότερες από μία ανεξάρτητες μεταβλητές και μία άγνωστη συνάρτηση αυτών των μεταβλητών
. Κανένας άλλος, εν ζωή, μαθηματικός δεν έχει συμβάλλει περισσότερο στην κατανόηση των μερικών διαφορικών εξισώσεων όσο ο αργεντινο-αμερικανός Luis A. Caffarelli. Ανακάλυψε έξυπνες νέες τεχνικές, ανέδειξε λαμπρή γεωμετρική διορατικότητα και έχει δώσει πολλά θεμελιώδη αποτελέσματα.
Γεννήθηκε στο Μπουένος Άιρες το 1948 και σπούδασε μαθηματικά στο πανεπιστήμιο του Μπουένος Άιρες. Υπό την επίβλεψη του Calixto Calderon, απέκτησε το διδακτορικό του το 1972 (τίτλος διατριβής: On conjugation and summability of Jacobi series) και το επόμενο έτος μετακόμισε στο πανεπιστήμιο της Μινεσότα ως μεταδιδακτορικός.
Στη Μινεσότα, ο Caffarelli άλλαξε την κατεύθυνση της έρευνάς του αφού παρακολούθησε μια σειρά διαλέξεων για την αρμονική ανάλυση που δόθηκε από τον Hans Lewy, έναν συνταξιούχο πολωνικής καταγωγής αμερικανό μαθηματικό. Ο Caffarelli ζήτησε από τον Lewy να του προτείνει μερικά προβλήματα για να ασχοληθεί και ο Lewy πρότεινε το «πρόβλημα εμποδίου». Ο Caffarelli έπρεπε να μάθει το θέμα από μηδενική βάση. Γρήγορα άρχισε να σημειώνει εκπληκτική πρόοδο στο θέμα και στην ευρύτερη περιοχή των «προβλημάτων ελεύθερων συνόρων».
Σαπουνόφουσκες και παγάκια
Το πρόβλημα του εμποδίου με το οποίο ο Caffarelli ξεκίνησε την έρευνά του είναι ένα στατικό πρόβλημα – δεν αλλάζει με την πάροδο του χρόνου. Τέτοιο παράδειγμα είναι η επιφάνεια μιας σαπουνόφουσκας που ως γνωστόν τείνει να γίνει όσο το δυνατόν μικρότερη. Για να υπολογίσει κανείς το σχήμα τέτοιων ελάχιστων επιφανειών, χρειάζεται διαφορικές εξισώσεις. Ο Caffarelli ενδιαφέρθηκε για το πώς συμπεριφέρονται οι ελάχιστες επιφάνειες όταν συναντούν ένα εμπόδιο. Ένα από τα πιο σημαντικά ερωτήματα όταν εξετάζουμε αυτό το πρόβλημα είναι το μέγεθος της επιφάνειας της περιοχής όπου η σαπουνόφουσκα και το εμπόδιο βρίσκονται σε επαφή. Διαισθητικά θα έλεγε κανείς ότι η επιφάνεια επαφής της φυσαλίδας έχει ένα ομαλό όριο χωρίς γωνίες ή προεξοχές. Αλλά η μαθηματική του απόδειξη είναι πολύ δύσκολη γιατί πρέπει να υπολογιστέι το ελάχιστο εμβαδόν που προκύπτει για όλα τα είδη εμποδίων, κάτι που απαιτεί την επίλυση ενός εξαιρετικά μεγάλου αριθμού εξαιρετικά περίπλοκων διαφορικών εξισώσεων. Ο Caffarelli ξεκίνησε την αντιμετώπιση αυτού του προβλήματος στη δεκαετία του 1970 εξετάζοντας τις ιδιότητες των διαφορικών εξισώσεων και διαπίστωσε ότι το όριο της επιφάνειας επαφής δεν έχει σχισμές ή γωνίες – εφόσον το εμπόδιο είναι επίσης ομαλό.
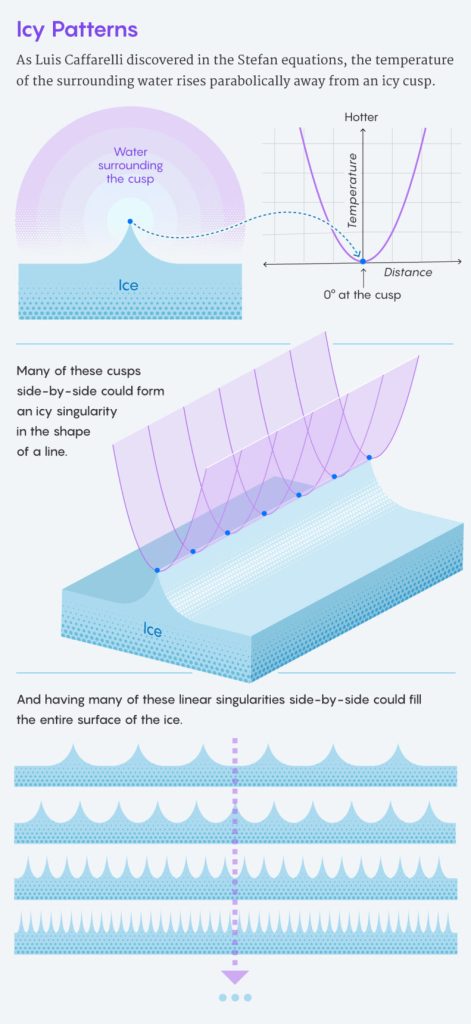
Αυτή η εργασία του έδωσε τη δυνατότητα να επικεντρωθεί σε πιο περίπλοκα φαινόμενα, όπως η περιγραφή της τήξης ενός κύβου πάγου στο νερό. Ο φυσικός Josef Stefan είχε ήδη ανοίξει το δρόμο στα τέλη του 19ου αιώνα σ’ αυτό το πρόβλημα καταλήγοντας σε δύο τύπους. Ο πρώτος περιγράφει την ροή της θερμότητας από το νερό προς τον πάγο, με αποτέλεσμα ο πάγος να θερμαίνεται και να αρχίζει να λιώνει. Ο δεύτερος αναφέρεται στην εξαφανιζόμενη επιφάνεια επαφής μεταξύ του νερού και του πάγου. Και οι δύο εξισώσεις συνδέονται: ο ρυθμός της μεταφοράς θερμότητας εξαρτάται από την επιφάνεια του πάγου, ενώ η ροή θερμότητας καθορίζει πόσο γρήγορα συρρικνώνεται η επιφάνεια.
To λιώσιμο του πάγου είναι το πιο σημαντικό παράδειγμα ενός προβλήματος «ελεύθερων ορίων», όπου διερευνάται πώς μια διαδικασία όπως η διάχυση της θερμότητας πραγματοποιείται στα όρια, που σ’ αυτή την περίπτωση, το όριο είναι μεταξύ πάγου και νερού. Οι εξισώσεις του Stefan φαινόταν να περιγράφουν καλά το πρόβλημα, αλλά μέχρι τη δεκαετία του 1970 η επίλυση των εξισώσεων δεν ήταν ξεκάθαρη. Τίποτε δεν εμπόδιζε τις εξισώσεις να οδηγήσουν σε απίθανα σενάρια,π.χ. σε ένα σχήμα πάγου που μοιάζει με φράκταλ, το οποίο δεν είχε παρατηρηθεί ποτέ στη φύση. Επρόκειτο για πολύ πιο δύσκολο πρόβλημα από το στατικό πρόβλημα της σαπουνόφουσκας, αφού το λιώσιμο του πάγου περιέχει και την μεταβλητή του χρόνου. Επιπλέον σύμφωνα με τις εξισώσεις σε ένα παγάκι κατά τη διαδικασία της τήξης του, εμφανίζονται ιδιομορφίες – κορυφές, γωνίες και προεξοχές – ακόμα κι αν το αρχικό σχήμα του πάγου ήταν ομαλό. Δεν έχετε παρά να φανταστείτε ένα παγάκι σε σχήμα κλεψύδρας: μόλις λιώσει το συνδετικό τμήμα, σχηματίζονται δύο παγάκια με προεξοχές, τουλάχιστον για μικρό χρονικό διάστημα.
Ο Caffarelli απέδειξε ότι υπάρχουν ιδιομορφίες στα μαθηματικά της τήξης του πάγου. Επινόησε επίσης και έναν τρόπο προσδιορισμού του αριθμού των ιδιομορφιών κατά μήκος του ορίου πάγου-νερού, χωρίς να τις ‘εξημερώσει’, συμβάλλοντας όμως στην απόδειξη ότι ο πάγος που λιώνει παραμένει ομαλός (βλέπε Mathematicians Prove Melting Ice Stays Smooth).
Το 1976 δημοσίευσε έξι εργασίες και το 1977 είχε την πρώτη του εργασία στο έγκριτο περιοδικό Acta Mathematica με τίτλο «The regularity of free boundaries in higher dimensions«. (Αξίζει να σημειωθεί ότι εκείνο το χρονικό διάστημα 1977 έως 1979, ο Ιωάννης Αθανασόπουλος, καθηγητής σήμερα στο τμήμα μαθηματικών του πανεπιστημίου Κρήτης, ολοκλήρωσε την διδακτορική του διατριβή υπό την καθοδήγηση του L.A. Caffarelli).
Το 1980 ο Caffarelli μετακόμισε στο ινστιτούτο Courant του πανεπιστημίου της Νέας Υόρκης, το οποίο ειδικεύεται στα εφαρμοσμένα μαθηματικά. Περπατώντας μια μέρα στην Chinatown με τον Robert Kohn και τον Louis Nirenberg (ο βραβευμένος με το βραβείο Abel 2015 -απεβίωσε το 2020), αποφάσισαν να συνεργαστούν σε ένα θέμα σχετικά με τις εξισώσεις Navier-Stokes, ένα σύνολο ΜΔΕ που περιγράφει την δυναμική των ρευστών. Το αποτέλεσμα αυτής της συνεργασίας ήταν η δημοσίευση του 1982 με τίτλο «Partial regularity of suitable weak solutions of the Navier-Stokes equations«, μια εργασία ορόσημο που αργότερα, το 2014, θα κέρδιζε το βραβείο Steele της Αμερικανικής Μαθηματικής Εταιρείας. Όταν ο Nirenberg ρωτήθηκε αργότερα για τον Caffarelli ως μαθηματικός, απάντησε: «Φανταστική διαίσθηση. Απίστευτη. ..Δυσκολεύτηκα να συμβαδίσω μαζί του. Κατά κάποιο τρόπο βλέπει αμέσως πράγματα που οι άλλοι άνθρωποι δεν βλέπουν».
Οι μερικές διαφορικές εξισώσεις Navier-Stokes περιγράφουν τη ροή των ρευστών. Οι εξισώσεις αυτές έχουν προκαλέσει ατέλειωτες συζητήσεις μεταξύ των μαθηματικών εδώ και αιώνες. Δεν είναι καν γνωστό ότι δίνουν πάντα μια πεπερασμένη και ομαλή λύση. Αυτό σημαίνει πως δεν είναι σαφές αν η ταχύτητα ροής μπορεί να αυξηθεί ξαφνικά σε κάποιο σημείο ή αν θα μπορούσε ακόμη να λάβει και απείρως μεγάλες τιμές. Αυτή η ερώτηση είναι ένα από τα επτά προβλήματα της Χιλιετίας, για τα οποία το ινστιτούτο Clay Mathematics προσέφερε βραβείο ενός εκατομμυρίου δολαρίων για την λύση του καθενός.
Οι Caffarelli, Kohn και Nirenberg έφτασαν σε ένα αποτέλεσμα που αντιπροσωπεύει την πιο σημαντική ανακάλυψη σε αυτόν τον τομέα μέχρι σήμερα: Αν οι λύσεις Navier-Stokes έπρεπε να περιέχουν ιδιομορφίες – ροές ρευστών που παρουσιάζουν ακανόνιστες μεταβολές ή απείρως μεγάλες ταχύτητες—αυτό θα σήμαινε ότι οι ιδιομορφίες προορίζονταν να εξαφανιστούν αμέσως. Αυτό το εύρημα δεν λύνει το σχετικό πρόβλημα του Millennium Prize, αλλά εγγυάται ότι, σύμφωνα με τις εξισώσεις, τα ρευστά θα συμπεριφέρονται με αυτόν τον περίεργο τρόπο, αν το κάνουν, για σύντομο χρονικό διάστημα – μια μεγάλη ανακούφιση για έναν σχεδιαστή αεροπλάνων ή αυτοκινήτων
Στις αρχές της δεκαετίας του ’80, ο Caffarelli είχε ήδη καθιερωθεί στην κοινότητα των μαθηματικών. Κέρδισε το βραβείο Guido Stampacchia το 1982 και το βραβείο Bôcher το 1984. Ο Caffarelli ήταν καθηγητής στο Πανεπιστήμιο του Σικάγο από το 1983 έως το 1986, και στη συνέχεια μετακόμισε για μια δεκαετία στο Ινστιτούτο Προηγμένων Σπουδών στο Πρίνστον. Κατά τη διάρκεια αυτής της περιόδου ασχολήθηκε κυρίως με την εξίσωση Monge-Ampère, μια άλλη γνωστή μη γραμμική ΜΔΕ, αναπτύσσοντας αυτό που τώρα ονομάζεται «θεωρία κανονικότητας του Caffarelli», που έχει σημαντικές εφαρμογές σε άλλους τομείς, όπως η θεωρία της βέλτιστης μεταφοράς.
Από το 1997 είναι καθηγητής μαθηματικών στο πανεπιστήμιο του Τέξας στο Ώστιν, όπου, μεταξύ άλλων εργασιών, έχει κάνει εντυπωσιακές προόδους στη θεωρία της ομογενοποίησης, ένα πεδίο έρευνας στις ΜΔΕ που εξετάζει φυσικές ιδιότητες σε διαφορετικές κλίμακες.
Ο Caffarelli δεν είναι μόνο αξιοσημείωτος για το βάθος του έργου του, είναι επίσης και εξαιρετικά παραγωγικός. Έχει δημοσιεύσει 320 εργασίες και, σε ηλικία 74 ετών, συνεχίζει να δημοσιεύει αρκετές εργασίες κάθε χρόνο. Είναι πολύ αγαπητός στην κοινότητα και έχει συν-γράψει εργασίες με περισσότερα από 130 άτομα. Οι εργασίες του Caffarelli είχαν 19.000 αναφορές, αριθμός που μαρτυρεί την επιρροή του στα σύγχρονα μαθηματικά, και είχε περισσότερους από 30 διδακτορικούς φοιτητές. Τιμήθηκε μεταξύ άλλων, με το βραβείο Rolf Schock 2005, το βραβείο Steele 2009 της Αμερικανικής Μαθηματικής Εταιρείας, το βραβείο Wolf 2012, το μετάλλιο Solomon Lefschetz 2013 και το βραβείο Shaw 2018.