φεγγάρι (5 άρθρα)

Γιατί αυξήθηκε η διάρκεια της ημέρας κατά 30 λεπτά από την εποχή των δεινοσαύρων;

27 Μαΐου 2021

Η Γη περιστρεφόταν ταχύτερα πριν από 70 εκατομμύρια χρόνια (στο τέλος της εποχής των δεινοσαύρων) σε σχέση με σήμερα. Η διάρκεια μιας ημέρας ήταν κατά μισή ώρα μικρότερη (23,5 ώρες αντί 24 ώρες) και το έτος περιλάμβανε 372 αντί για 365 ημέρες.

Αυτό ήταν γνωστό, αλλά επιβεβαιώνεται και από το συμπέρασμα μιας νέας επιστημονικής έρευνας, που βασίστηκε στη μελέτη των απολιθωμάτων ενός αρχαίου μαλάκιου (κάτι σαν αχιβάδα) της ύστερης κρητιδικής περιόδου. Οι ερευνητές, με επικεφαλής τον γεωχημικό Νιλς ντε Βίντερ του Ελευθέρου Πανεπιστημίου των Βρυξελλών, δημοσιεύουν τα αποτελέσματά τους στην εργασία τους με τίτλο: «Subdaily‐Scale Chemical Variability in a Torreites Sanchezi Rudist Shell: Implications for Rudist Paleobiology and the Cretaceous Day‐Night Cycle».

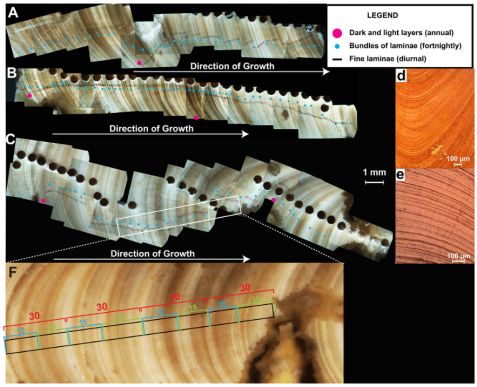
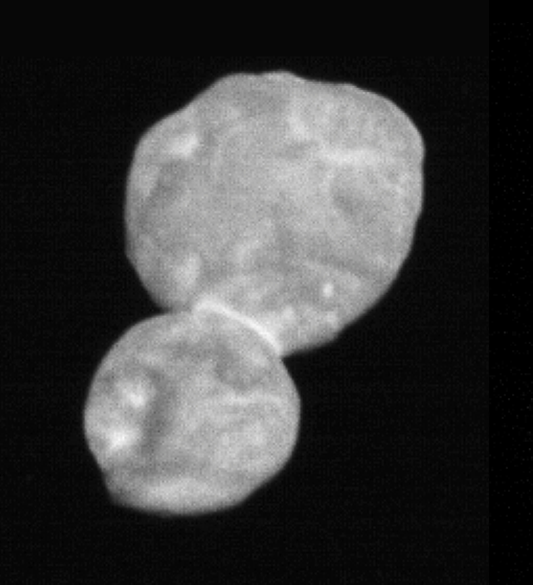
Το αρχαίο μαλάκιο βρέθηκε στα σημερινά βουνά του Ομάν (μια περιοχή που τότε ήταν τροπικά ρηχά νερά), αναπτυσσόταν γρήγορα και κάθε ημέρα προσέθετε στο σώμα του δακτυλίους ανάπτυξης, όπως συμβαίνει με τους κορμούς των δέντρων, κάτι που επιτρέπει τη δενδροχρονολόγηση. Οι επιστήμονες χρησιμοποίησαν λέιζερ για να μετρήσουν με ακρίβεια τους δακτυλίους αυτούς και να κάνουν νέες εκτιμήσεις για τη διάρκεια της ημέρας πριν από 70 εκατ. χρόνια. Επιπλέον, η ανάλυση δείχνει ότι οι θερμοκρασίες των ωκεανών εκείνης της εποχής ήταν πολύ υψηλότερες από τις σημερινές, φθάνοντας ακόμη και τους 40 βαθμούς Κελσίου το καλοκαίρι και ξεπερνώντας τους 30 βαθμούς τον χειμώνα. Τα εν λόγω μαλάκια εξαφανίστηκαν μαζί με τους δεινόσαυρους της ξηράς μετά την πτώση μεγάλου αστεροειδούς στην περιοχή του Μεξικού, πριν από 66 εκατ. έτη.

Οι επιστήμονες χρησιμοποίησαν ένα λέιζερ για να δημιουργήσουν μικροσκοπικές τρύπες στο μαλάκιο και στη συνέχεια να ερευνήσουν για ίχνη στοιχείων. Αυτά, με τη σειρά τους, παρείχαν πληροφορίες για τη θερμοκρασία και τη χημική σύνθεση του νερού. «Έχουμε τέσσερα έως πέντε στοιχεία την ημέρα, κάτι που σπάνια εξασφαλίζεις στη γεωλογική ιστορία», εξηγεί ο επικεφαλής της έρευνας Νιλς ντε Βίντερ, ο γεωχημικός του Πανεπιστημίου των Βρυξελλών που έκανε την ανακοίνωση. «Βασικά, μπορούμε να δούμε μία ημέρα πριν από 70 εκατ. χρόνια». Επειδή το αρχαίο απολίθωμα εμφάνιζε μεγάλες εποχικές διαφοροποιήσεις ή αλλαγές στο μαλάκιο, οι ερευνητές κατάφεραν να αναγνωρίσουν τις εποχές και να μετρήσουν τα χρόνια.

Ενώ λοιπόν η διάρκεια του έτους δεν έχει αλλάξει κατά την εξέλιξη της Γης, ο αριθμός των ημερών του έτους συνεχώς μικραίνει, καθώς οι ημέρες μεγαλώνουν, κάτι που οφείλεται στην επιβράδυνση της περιστροφής του πλανήτη μας. Έτσι, η διάρκεια της ημέρας αυξάνεται και από 23,5 ώρες που ήταν προς το τέλος της εποχής των δεινοσαύρων, έγινε 24 ώρες.

Γιατί όμως η ιδιο-περιστροφή (σπιν) της Γης, έστω και αργά, επιβραδύνεται; Διότι, λέει, η Σελήνη απομακρύνεται με ρυθμό 3,82 εκατοστών ετησίως.
Και γιατί απομακρύνεται η Σελήνη; Γιατί η απομάκρυνση της Σελήνης επηρεάζει την ιδιο-περιστροφή της Γης;

Τα ερωτήματα αυτά μπορούν να εξηγηθούν με τις αρχές διατήρησης στροφορμής και ενέργειας του συστήματος Γης-Σελήνης.

Η στροφορμή Γης-Σελήνης ως προς το κέντρο μάζας του συστήματος (που για ευκολία θα θεωρήσουμε ότι ταυτίζεται με το κέντρο μάζας της Γης) θα είναι:

$\vec{L}=\vec{L}_{\Gamma} + \vec{L}_{\Sigma} + M_{\Sigma}\, \vec{r} \times \vec{v}$ (1)

όπου L_Γ και L_Σ οι ιδιο-στροφορμές Γης και Σελήνης, ενώ ο τελευταίος όρος εκφράζει την τροχιακή στροφορμή της Σελήνης, Μ_Σ είναι η μάζα της Σελήνης, υ η ταχύτητα της Σελήνης στην τροχιά γύρω από τη Γη, και r η απόσταση Γης-Σελήνης. Μπορούμε να χρησιμοποιήσουμε την παραπάνω εξίσωση αν κάνουμε μερικές εύλογες υποθέσεις: Πρώτα να υποθέσουμε ότι η τροχιά της Σελήνης γύρω από τη Γη είναι κυκλική ακτίνας r. Δεύτερον να υποθέσουμε ότι ο άξονας γύρω από τον οποίο περιστρέφεται η Γη είναι κάθετος στο επίπεδο της τροχιάς της Σελήνης, οπότε η τροχιακή στροφορμή της Σελήνης θα είναι ομόρρροπη με την ιδιο-στροφορμή της Γης. Επιπλέον, στην παραπάνω εξίσωση μπορούμε να αγνοήσουμε την στροφορμή λόγω ιδιοπεριστροφής της Σελήνης διότι είναι πολύ μικρή σε σχέση με τους άλλους όρους

Αν θεωρήσουμε τη Γη ομογενή σφαίρα, τότε η στροφορμή εξαιτίας της περιστροφής γύρω από τον άξονά της θα είναι:
L_Γ=Ι_Γ ω_Γ=2/5 Μ_ΓR_Γ²2π/Τ_Γ=7·10³³ J·s, για R_Γ=6400km, Μ_Γ=6·10²⁴kg και Τ_Γ=24h.
Κάνοντας παρόμοιο υπολογισμό για την ιδιο-περιστροφή της Σελήνης παίρνουμε L_Σ=Ι_Σ ω_Σ=2/5 Μ_ΣR_Σ²2π/Τ_Σ=2,3·10²⁹ J·s, για R_Σ=1700km, Μ_Σ=7,3·10²²kg και Τ_Σ=27,3d.
H τροχιακή στροφορμή της Σελήνης ισούται με L_τρ,Σ=Μ_Σ ω_Σr²=2,9·10³⁴ J·s, όπου r=385.000 km και ω_Σ=2π/Τ_Σ, με Τ_Σ=27,3d. Παρατηρούμε ότι η στροφορμή της Σελήνης εξαιτίας της ιδιο-περιστροφής της είναι πέντε τάξεις μεγέθους μικρότερη σε σχέση με τους άλλους δυο όρους στην εξίσωση (1). Οι στροφορμές που υπολογίστηκαν παραπάνω βρίσκονται σε πολύ καλή συμφωνία μ’ αυτές που δίνει το πρόγραμμα Wolfram Alpha.

Αν αγνοήσουμε την ανομοιογένεια του βαρυτικού πεδίου του ήλιου σε όλη την έκταση του συστήματος Γης-Σελήνης και θεωρήσουμε ότι η εξωτερική βαρυτική δύναμη από τον ήλιο διέρχεται από το κέντρο μάζας του συστήματος, τότε η ροπή της είναι μηδέν. Έτσι, σύμφωνα με την αρχή διατήρησης της στροφορμής, η στροφορμή του συστήματος Γης-Σελήνης διατηρείται σταθερή και σύμφωνα με τις παραπάνω υποθέσεις η εξίσωση (1) γράφεται:

L_Γης+ L_{τροχ,Σελήνης}= Ι_Γ ω_Γ+ Μ_Σ ω_Σr²= σταθερή (2)

Όμως, για μεγάλες χρονικές περιόδους οι όροι της τελευταίας εξίσωσης μεταβάλλονται. Ένας από τους κυριότερους λόγους είναι η ύπαρξη της παλιρροϊκής τριβής. Η απώλεια ενέργειας από τις παλίρροιες έχει ως αποτέλεσμα την σταδιακή επιβράδυνση της περιστροφής της Γης. Καθώς η Γη περιστρέφεται, επιχειρεί να μεταφέρει μαζί της και τις παλιρροϊκές «παραμορφώσεις» της, ενώ η έλξη της Σελήνης τις ωθεί πίσω στην ευθυγράμμιση. Ασκείται ένα ζεύγος δυνάμεων που επιβραδύνει την περιστροφή της Γης. Επειδή όμως η στροφορμή του συστήματος διατηρείται σταθερή, περιμένουμε αντίστοιχη αύξηση της τροχιακής στροφορμής της Σελήνης, άρα αύξηση της απόστασης Γης-Σελήνης.

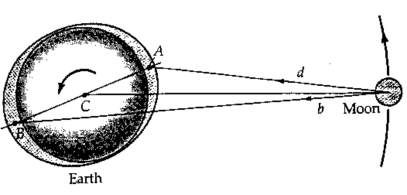Ας δούμε τα πράγματα διαφορετικά … παρακολουθώντας την Σελήνη. Εξαιτίας των παλιρροϊκών εξογκωμάτων προκύπτει μια μικρή επιτρόχια δύναμη, η οποία την επιταχύνει, απομακρύνοντάς την από τη Γη, αυξάνοντας την τροχιακή στροφορμή της και την ενέργειά της. Έτσι, η Σελήνη αυξάνει την τροχιακή της στροφορμή σε βάρος της ιδιο-στροφορμής της Γης – μειώνεται η γωνιακή ταχύτητα της Γης, άρα αυξάνεται η περίοδος περιστροφής της, δηλαδή η διάρκεια της ημέρας [1].

Το αποτέλεσμα είναι η Σελήνη να απομακρύνεται με ρυθμό 3,82 cm/έτος, ενώ η διάρκεια της ημέρας να μεγαλώνει ελάχιστα – αυξήθηκε κατά 30 λεπτά στα τελευταία … 70 εκατομμύρια χρόνια.

[1] Εφόσον η κίνηση της Σελήνης γύρω από τη Γη προσεγγίζεται ως ομαλή κυκλική, η βαρυτική έλξη μεταξύ Γης-Σελήνης παίζει τον ρόλο της κεντρομόλου δύναμης: $G \frac{M_{\Gamma} M_{\Sigma}}{r^{2}}= M_{\Sigma}\omega_{\Sigma}^{2}r$ ή $\omega_{\Sigma}=\sqrt{\frac{GM_{\Gamma}}{r^{3}}}$ . Αντικαθιστώντας στην εξίσωση (2) παίρνουμε μετά από πράξεις: $\omega_{\Gamma}=c_{1}-c_{2}\sqrt{r}$ , όπου c₁ και c₂ θετικές σταθερές. Παρατηρούμε λοιπόν ότι καθώς η απόσταση r μεταξύ Γης-Σελήνης αυξάνεται η γωνιακή ταχύτητα περιστροφής της Γης μειώνεται (και η περίοδος αυξάνεται), ενώ το ίδιο συμβαίνει και με την γωνιακή ταχύτητα περιφοράς της Σελήνης.

Πηγή

Κατηγορίες:

Φυσική & Φιλοσοφία

Tags: στροφορμή, γη, σελήνη, φεγγάρι, διάρκεια ημέρας

Γιατί δεν είναι όλοι βέβαιοι ότι ο άνθρωπος πάτησε στη Σελήνη;

14 Ιανουαρίου 2020

| 0 ΣΧΟΛΙΑ

του Αλέξη Δεληβοριά

Στις 16 Ιουλίου [2009] συμπληρώθηκαν 40 χρόνια από την εκτόξευση του θρυλικού Apollo 11. Τα λόγια που διατύπωσε ο αμερικανός αστροναύτης Neil Armstrong πατώντας για πρώτη φορά το πόδι του στο σεληνιακό έδαφος θα μείνουν για πάντα χαραγμένα στην Ιστορία: ένα μικρό βήμα για τον άνθρωπο, ένα γιγάντιο άλμα για την ανθρωπότητα (για περισσότερες πληροφορίες δες Θέμα Ιουλίου 2006 ).

Την εντυπωσιακή επιτυχία της αποστολής του Apollo 11 ακολούθησαν 5 ακόμη επιτυχείς προσεδαφίσεις στην επιφάνεια της Σελήνης.

Με την ολοκλήρωση και της τελευταίας, εκείνης του Apollo 17, συνολικά 12 αστροναύτες περπάτησαν στην επιφάνεια του φυσικού μας δορυφόρου, πραγματοποίησαν πειράματα και συνέλεξαν σεληνιακά πετρώματα για μελλοντική ανάλυση.

Και όμως, εάν πιστέψουμε ορισμένους αυτοαποκαλούμενους «ερευνητές», τίποτε απ’ όλα αυτά δεν συνέβη, αφού σύμφωνα με τα λεγόμενά τους η NASA δεν διέθετε την απαραίτητη τεχνολογία για να πραγματοποιήσει επανδρωμένες αποστολές στη Σελήνη!
Πρόκειται για μια από τις περισσότερο δημοφιλείς θεωρίες συνωμοσίας όλων των εποχών.

Σύμφωνα με αυτή, οι χιλιάδες φωτογραφίες από τη Σελήνη στην πραγματικότητα ελήφθησαν σε μια μυστική τοποθεσία στη Γη σε ένα αριστοτεχνικά στημένο κινηματογραφικό στούντιο στην περίφημη Περιοχή 51, στην έρημο της Νεβάδα.

Τα εκατοντάδες κιλά σεληνιακών πετρωμάτων που υποτίθεται ότι μετέφεραν στη Γη οι 12 αστροναύτες των επανδρωμένων αποστολών του Προγράμματος Apollo στην πραγματικότητα είναι γήινα πετρώματα ή «κατασκευάστηκαν» στο εργαστήριο. Οι 12 αστροναύτες ψεύδονται όταν ισχυρίζονται ότι περπάτησαν στη Σελήνη.

Δεκάδες πολιτικοί, εκατοντάδες επιστήμονες, χιλιάδες τεχνικοί, μηχανικοί και υπάλληλοι της NASA συμμετείχαν στη μεγαλύτερη συγκάλυψη στην ιστορία της ανθρωπότητας εξυφαίνοντας μια ασύλληπτων διαστάσεων παγκόσμια συνωμοσία, βασικός στόχος της οποίας ήταν να πείσει τους Αμερικανούς πολίτες και τον υπόλοιπο κόσμο ότι οι Σοβιετικοί διέθεταν υποδεέστερη διαστημική τεχνολογία και ότι οι Αμερικανοί ήταν εκείνοι που πήγαν πρώτοι στη Σελήνη.

Το πλήρωμα της μοιραίας αποστολής του Apollo 1, οι Roger Chaffee, Ed White και Gus Grissom, στην πραγματικότητα δολοφονήθηκαν από τη NASA, επειδή ήταν έτοιμοι να αποκαλύψουν την «αλήθεια», ότι δηλαδή οι αμερικανοί αστροναύτες δεν πήγαν στη Σελήνη ποτέ και ότι όλο το Πρόγραμμα Apollo ήταν μια αριστοτεχνικά στημένη απάτη, μια συνωμοσία εξυφασμένη στα υψηλότερα κλιμάκια της Αμερικανικής κυβέρνησης.

Οι ισχυρισμοί των συνωμοσιολόγων που υποστηρίζουν τη «μεγάλη φάρσα της Σελήνης» μπορούν εύκολα να αντιμετωπιστούν αρκεί να επικαλεστεί κανείς την κοινή λογική και να αναλύσει λίγο πιο προσεκτικά την ισχύ των επιχειρημάτων τους. Και πρώτα απ’ όλα να αναγνωρίσει ότι αυτοί οι ίδιοι οι αυτοαποκαλούμενοι «ερευνητές» έχουν ήδη προαποφασίσει για το τι πραγματικά συνέβη και ερμηνεύουν στοιχεία, δεδομένα και φωτογραφίες με τον τρόπο που τους «βολεύει» προσπαθώντας να τα προσαρμόσουν στην ήδη διαμορφωθείσα θέση τους.

Κανενός είδους επιχείρημα δεν πρόκειται να αλλάξει την ήδη ειλημμένη απόφασή τους. Αυτό όμως αναιρεί την ίδια την επιστημονικότητα που επικαλούνται ότι διαθέτουν, αφού ένας πραγματικός επιστήμονας δεν προσπαθεί «πάση θυσία» να προσαρμόσει τα όποια επιστημονικά δεδομένα με τρόπο που να βολεύει τη γνώμη που έχει διαμορφώσει για κάποιο θέμα, αλλά αντίθετα θα πρέπει να διαθέτει και την απαραίτητη ευρύτητα πνεύματος ώστε να έχει το θάρρος να παραδεχτεί ότι κάπου σφάλλει.

Ακόμη και σήμερα, εκατομμύρια άνθρωποι σε Αμερική και Ευρώπη εξακολουθούν να πιστεύουν τους ισχυρισμούς ορισμένων «ερευνητών», οι οποίοι υποστηρίζουν ότι έχουν ανακαλύψει όλες εκείνες τις απαραίτητες αποδείξεις που αποκαλύπτουν τη σκοτεινή πλεκτάνη.

Προεξάρχουσα θέση στους ανά τον κόσμο συνωμοσιολόγους είχε μέχρι το θάνατό του κάποιος Bill Kaysing, ο οποίος από τη στιγμή που εμφανίστηκε στην εκπομπή

«Θεωρία συνωμοσίας: Πήγαμε στη Σελήνη;» που μεταδόθηκε από το αμερικανικό τηλεοπτικό κανάλι Fox στις 15 Φεβρουαρίου 2001 αναδείχθηκε σε ηγετική μορφή του ρεύματος αμφισβήτησης του κορυφαίου εκείνου επιτεύγματος της NASA.

Τα επιχειρήματα που επικαλούνται οι διάφοροι Kaysings αυτού του κόσμου δεν αντέχουν σε μια στοιχειωδώς σοβαρή εξέταση.

Γιατί, κατ’ αρχήν, θα πρέπει να σημειωθεί ότι όλες οι επιστημονικά προηγμένες χώρες της εποχής είχαν την τεχνολογική δυνατότητα να διαπιστώσουν εάν πραγματοποιήθηκαν ή όχι οι επανδρωμένες αποστολές της NASA στη Σελήνη με την ανίχνευση και μόνο των εκπομπών ήχου και εικόνας μεταξύ των διαστημοσυσκευών και του Κέντρου Ελέγχου.

Στα μέσα του Ψυχρού Πολέμου ειδικότερα, η Σοβιετική Ένωση είχε κάθε συμφέρον να καταγγείλει την υποτιθέμενη απάτη εάν όντως είχε στοιχεία για κάτι τέτοιο.

Το κύριο χαρακτηριστικό μιας επιτυχημένης συνωμοσίας αυτού του τύπου είναι να την γνωρίζουν όσο το δυνατό λιγότεροι άνθρωποι, αλλιώς η διαρροή και αποκάλυψή της είναι δεδομένη.

Τι συμβαίνει όμως σε αυτήν την περίπτωση; Υπάρχουν οι 12 αστροναύτες που πάτησαν το πόδι τους στη Σελήνη, χιλιάδες επιστήμονες, τεχνικοί, μηχανικοί και υπάλληλοι της NASA που σχεδίασαν και κατασκεύασαν τις διαστημοσυσκευές Apollo και τους πυραύλους Saturn του Προγράμματος Apollo και που παρακολούθησαν και κατέγραψαν βήμα-βήμα την αποστολή των διαστημοσυσκευών προς και από τη Σελήνη.

Έχουμε επίσης τους επιστήμονες, μηχανικούς και τεχνικούς των Σοβιετικών που για τους δικούς τους λόγους έκαναν ακριβώς το ίδιο.

Και εάν αυτό δεν σας είναι αρκετό, έχουμε τις χιλιάδες των επιστημόνων από εκατοντάδες ερευνητικά κέντρα και πανεπιστήμια παγκοσμίως, τα οποία δεν ελέγχονται από την Αμερικανική Κυβέρνηση, οι οποίοι μελέτησαν τα δείγματα των σεληνιακών πετρωμάτων και δημοσίευσαν τα αποτελέσματα των μελετών τους σε έγκυρα επιστημονικά περιοδικά, χωρίς ούτε ένας από αυτούς να αμφισβητήσει την προέλευσή τους.

Και πώς θα μπορούσε άλλωστε;

Τα σεληνιακά δείγματα που μας επέστρεψαν οι αμερικανοί αστροναύτες διαφέρουν κατά πολύ από τα πετρώματα που απαντούν στη Γη, τα οποία συγκριτικά εμπεριέχουν περισσότερο νερό στην κρυσταλλική τους δομή και δεν μπορούν να «κατασκευαστούν» στο εργαστήριο.

Επί πλέον, η χημική ανάλυση των κομματιών πυροκλαστικού γυαλιού που εντόπισαν οι αστροναύτες του Προγράμματος Apollo στη Σελήνη προσδιόρισε την ηλικία τους στα τουλάχιστον 3 δισεκατομμύρια έτη. Στη Γη, αντίθετα, τέτοιο ηφαιστειακό γυαλί, έπειτα από λίγα μόλις εκατομμύρια χρόνια θα παρουσίαζε εμφανή ίχνη διάβρωσης εξαιτίας του νερού που υπάρχει στη Γη. Τέτοια ίχνη διάβρωσης δεν εντοπίστηκαν από τους εκατοντάδες ανεξάρτητους επιστήμονες που τα μελέτησαν.

Εντοπίστηκε αντιθέτως κάτι άλλο, που θα ήταν αδύνατο να συμβεί με τις συνθήκες που επικρατούν στον πλανήτη μας. Η επιφάνεια των σεληνιακών δειγμάτων καλύπτεται από αναρίθμητους μικροσκοπικούς «κρατήρες» που σχηματίστηκαν κατά το βομβαρδισμό τους από μικρομετεωρίτες.

Κάτι τέτοιο θα μπορούσε να συμβεί μόνο σε περιβάλλον με ελάχιστη ή καθόλου ατμόσφαιρα.

Αν και αυτές οι μικροσκοπικές διαστημικές βολίδες κινούνται στο διάστημα με ταχύτητες που υπερβαίνουν τα 50.000 χιλιόμετρα την ώρα, καθώς εισέρχονται στη γήινη ατμόσφαιρα αναφλέγονται εξαιτίας της τριβής, γι’ αυτό και τα μικροσκοπικά αυτά βαθουλώματα απουσιάζουν παντελώς από τα γήινα πετρώματα.

Επειδή η Σελήνη αντίθετα δεν έχει πυκνή ατμόσφαιρα για να την προστατέψει, τα μικροσκοπικά αυτά σωματίδια χτυπούν τους επιφανειακούς της βράχους σκάβοντας αυτούς τους χαρακτηριστικούς κρατήρες-μινιατούρες, οι οποίοι είναι ορατοί στο μικροσκόπιο.

Ορισμένοι θα αντιτάξουν ότι τα σεληνιακά δείγματα ήταν εντέλει σεληνιακοί μετεωρίτες που τους βρήκε η NASA στην Ανταρκτική. Ούτε όμως η εξήγηση αυτή στέκει γιατί πολύ απλά οι μικροσκοπικοί αυτοί κρατήρες θα είχαν εξαφανιστεί με την ανάφλεξη των σεληνιακών μετεωριτών κατά την είσοδό τους στη γήινη ατμόσφαιρα.

Ένα άλλο γεγονός που αποδεικνύει ότι οι επανδρωμένες αποστολές στη Σελήνη ήταν πραγματικότητα είναι και το εξής: ο Neil Armstrong στον ιστορικό του περίπατο στην επιφάνεια της Σελήνης εγκατέστησε έναν ειδικό ανακλαστήρα laser, προκειμένου να υπολογιστεί ο χρόνος που χρειάζεται μια δέσμη laser για να φτάσει από τη Γη στη Σελήνη και ως εκ τούτου να υπολογιστεί η απόσταση που χωρίζει το φυσικό μας δορυφόρο από τον πλανήτη μας.

Το συγκεκριμένο πείραμα λειτουργεί ακόμα και σήμερα (Lunar Laser Ranging Experiment) και έχει μάλιστα επιβεβαιώσει ότι η Σελήνη απομακρύνεται από τον πλανήτη μας κατά 4 περίπου εκατοστά το χρόνο.

Οι θιασώτες των θεωριών συνωμοσίας επικαλούνται ως αδιάσειστο στοιχείο της συνωμοσίας και το γεγονός ότι στις φωτογραφίες που ελήφθησαν στη Σελήνη απουσιάζουν παντελώς τα άστρα από τον σκοτεινό σεληνιακό ουρανό.

Αυτό είναι μάλιστα ένα από τα βασικά τους επιχειρήματα και ίσως το πιο εύκολο να καταρριφθεί. Αν παραδεχτούμε προς στιγμή ότι το επιχείρημα αυτό στέκει θα πρέπει να αποδεχτούμε επίσης ότι ένας ερευνητικός οργανισμός του μεγέθους της NASA «ξέχασε» να συμπεριλάβει άστρα στις «στημένες» φωτογραφίες της σελήνης, πράγμα προφανώς απίθανο εάν αναλογιστεί κανείς τις πολιτικές και στρατιωτικές πιέσεις των πανίσχυρων εμπνευστών της συνωμοσίας που θα απαιτούσαν η απάτη να είναι τέλεια και οι όποιες πλαστές φωτογραφίες να φαίνονται επιστημονικά έγκυρες.

Θα πρέπει να πιστέψουμε δηλαδή ότι η NASA δεν ήταν μόνο ανίκανη να στείλει αστροναύτες στη Σελήνη, αλλά ήταν και εντελώς ανίκανη να «στήσει» μια πιστευτή και «επιστημονικά έγκυρη» κινηματογραφική παραγωγή-απάτη.

Φυσικά η πραγματικότητα είναι πολύ πιο απλή: τα άστρα υπάρχουν, απλά είναι πολύ αμυδρά για να αποτυπωθούν σε φιλμ. Οι περισσότεροι φωτογράφοι ήδη γνωρίζουν την αιτία. Είναι αδύνατο να αποτυπωθεί συγχρόνως στην ίδια φωτογραφική πλάκα κάτι πολύ φωτεινό και κάτι πολύ αμυδρό.

Το σεληνιακό έδαφος και οι κάτασπρες στολές των αστροναυτών φωτίζονται έντονα από τον Ήλιο, γι’ αυτό και η φωτογραφική κάμερα που θα τα αποτυπώσει θα πρέπει να ρυθμιστεί κατάλληλα: όπως ακριβώς η ίριδα του ματιού μας συστέλλεται σε ένα έντονα φωτεινό περιβάλλον, έτσι και το διάφραγμα της φωτογραφικής κάμερας θα πρέπει να ρυθμιστεί κατά τέτοιον τρόπο ώστε η έκθεση του φιλμ στο φως να είναι σύντομη.

Τα άστρα στο σεληνιακό ουρανό όμως είναι τόσο αμυδρά που δεν προλαβαίνουν να καταγραφούν στο φιλμ στο σύντομο αυτό χρονικό διάστημα. Για να αποτυπωθούν, θα έπρεπε αντίθετα το διάφραγμα να μείνει ανοικτό για αρκετά μεγαλύτερο χρονικό διάστημα. Τότε όμως, η φωτεινότητα των λαμπερών αντικειμένων που προσπαθούμε να αποτυπώσουμε θα «κατέστρεφε» τη φωτογραφία μας.

Είναι απλά αδύνατο να καταγραφούν στην ίδια φωτογραφία δύο αντικείμενα με πολύ μεγάλη διαφορά φωτεινότητας.

Δεν θα συνεχίσουμε εδώ την προσπάθεια κατάρριψης των αρκετών ακόμα «επιχειρημάτων» που επικαλούνται οι διάφοροι συνωμοσιολόγοι, καθώς μια απλή έρευνα στο διαδίκτυο εντοπίζει πολλούς δικτυακούς τόπους, οι οποίοι έχουν κάνει εξαιρετική δουλειά σε αυτόν τον τομέα.

Θα επικαλεστούμε αντίθετα τη γνώμη που εξέφρασε ο James Van Allen, ο επιστήμονας που εντόπισε τις Ζώνες Van Allen, όπως ονομάστηκαν προς τιμή του, όταν έμαθε ότι σύμφωνα με τους συνωμοσιολόγους το ταξίδι στη Σελήνη ήταν ανέφικτο εξαιτίας της θανατηφόρας δόσης ακτινοβολίας που θα απορροφούσαν οι αστροναύτες: «η πρόσφατη εκπομπή που είδα στο FOX είναι ένα εφευρετικό και διασκεδαστικό συνονθύλευμα ανοησίας. Ο ισχυρισμός ότι η έκθεση στην ακτινοβολία στη διάρκεια των αποστολών Apollo θα ήταν θανατηφόρα για τους αστροναύτες είναι ένα μόνο παράδειγμα αυτής της ανοησίας».

Πηγή: eef.edu.gr (Ευγενίδειο Πλανητάριο)

Κατηγορίες:

Ιστορία

Tags: σελήνη, NASA, αστροναύτες, φεγγάρι, θεωρία συνωμοσίας, Apollo 11

Οι ήχοι πλανητών και λοιπών ουρανίων σωμάτων, όπως τους κατέγραψε η NASA!

3 Οκτωβρίου 2019

| 0 ΣΧΟΛΙΑ

Η Φυσική των διαστημικών ήχων

Πώς «ακούγονται» οι πλανήτες και τα λοιπά ουράνια σώματα;

Στην πραγματικότητα, οι πλανήτες δεν παράγουν ήχους που μπορεί κανείς να ακούσει όντας κοντά τους.

Εξάλλου, στο διάστημα δεν υπάρχει ατμόσφαιρα, πόσο, μάλλον, ατμόσφαιρα με επαρκή πυκνότητα για τη διάδοση του ήχου. Ο ήχος δεν μπορεί να διαδοθεί με τον τρόπο που διαδίδεται εντός της γήινης ατμόσφαιρας, δηλαδή με τη μορφή [ηχητικών] διαμηκών κυμάτων.

Εντούτοις, όλα τα ουράνια σώματα και, μεταξύ αυτών, και οι πλανήτες, εκπέμπουν ακτινοβολίες σε όλο το φάσμα δυνατών εκπομπών. Εξ αυτού, ένα μικρό μόνο τμήμα είναι ορατό στον άνθρωπο.
Με κατάλληλη επεξεργασία από τους επιστήμονες της όμως, η NASA αποκωδικοποίησε ένα άλλο, μικρό, τμήμα αυτών των εκπομπών, καθιστώντας τες ακροάσιμες από τον άνθρωπο.

Πώς ακούγονται πλανήτες και άλλα ουράνια σώματα;

Στα βίντεο που ακολουθούν θα ακούσετε απόκοσμες δονήσεις από το Φεγγάρι, τον Ήλιο, τον Κρόνο, τον Ποσειδώνα, το Δία, τον Ουρανό αλλά και τη Γη!

Κατηγορίες:

Φυσική & Φιλοσοφία

Tags: γη, διάστημα, NASA, ήχος, ήλιος, Πλανήτες, φεγγάρι, Αστρονομία, Κρόνος, Δίας, ουρανός, πλανήτης, Ποσειδώνας

Πώς μετράμε το ύψος ενός βουνού της Σελήνης;

31 Μαΐου 2019

| 0 ΣΧΟΛΙΑ

Εικόνα: Φωτογραφία της Σελήνης από ένα ερασιτεχνικό τηλεσκόπιο, όταν η Σελήνη βρίσκεται στη φάση του πρώτου τετάρτου. Παρατηρείστε τα φωτεινά σημεία Α και Β στη σκοτεινή περιοχή. Πρόκειται για κορυφές σεληνιακών βουνών στις οποίες φτάνει το φως του ήλιου!

Μπορούμε να εκτιμήσουμε το ύψος των βουνών στα οποία ανήκουν οι κορυφές Α και Β των βουνών που βρίσκονται στη Σελήνη; Η απάντηση είναι καταφατική δεδομένου ότι υπάρχει μια απλή, αλλά ευφυής ιδέα, που οφείλεται στον Γαλιλαίο.

Εξαιτίας του σφαιρικού σχήματος της Σελήνης, το φως του ήλιου αγγίζει πρώτα τις κορυφές των βουνών (π.χ. τα φωτεινά σημεία Α και Β στην εικόνα 1) πριν φτάσει στους πρόποδές τους. Αυτό συμβαίνει κοντά στο όριο που χωρίζει την σκοτεινή από την φωτεινή περιοχή της εικόνας. Ας σημειωθεί ότι οι οι ακτίνες του ήλιου είναι εφαπτόμενες στην επιφάνεια της Σελήνης στο νοητό τόξο που αποτελεί το όριο μεταξύ σκοτεινής-φωτεινής περιοχής. Αυτή η γεωμετρία απεικονίζεται (και προφανώς όχι σε κλίμακα) στο σχήμα 2(α):

Σχήμα 2

Στο σχήμα 2(α), ο σεληνιακός δίσκος παριστάνεται με έναν κύκλο με κέντρο O. Η γραμμή XY είναι ακτίνα φωτός από τον ήλιο, εφαπτόμενη στον κύκλο στο σημείο Χ και περνάει από την κορυφή του βουνού Y. Η διάμετρος XW είναι το όριο σκιάς-φωτός (στη φάση του πρώτου τετάρτου της σελήνης).

Το σημείο Ζ βρίσκεται στην ευθεία OY και |ΟΧ| = |OZ|= r, όπου r είναι η ακτίνα της Σελήνης. Το ακτινικό τμήμα OX είναι κάθετο στην εφαπτομένη XY – όπως ξέρουμε από τη γεωμετρία. Έτσι, εφαρμόζοντας το Πυθαγόρειο θεώρημα στο ορθογώνιο τρίγωνο OXY, παίρνουμε για το ύψος H του όρους ΥΖ:

όπου d=r/|ΧΥ|, και η ακτίνα της Σελήνης θεωρείται γνωστή (r≈1736 km), αφού μπορεί να υπολογιστεί με μια μέθοδο γνωστή από την αρχαιότητα. Για να προσδιορίσουμε το ύψος H του σεληνιακού βουνού αρκεί να βρούμε την τιμή του d.

Το d μπορεί να υπολογιστεί έμμεσα από την φωτογραφία χρησιμοποιώντας την ομοιότητα τριγώνων. Σημειώστε ότι κατά τη φάση του πρώτου τετάρτου, η γη, το βουνό στη Σελήνη και το πλησιέστερο σημείο στο όριο μεταξύ σκοτεινής-φωτεινής περιοχής, σχηματίζουν ένα ορθογώνιο τρίγωνο, βλέπε σχήμα 2(β). Επομένως, οι αποστάσεις στη Σελήνη μειώνονται αναλογικά στη φωτογραφία. Συγκεκριμένα, η τιμή d=r/|XY| είναι η ίδια, είτε υπολογίζεται χρησιμοποιώντας τα πραγματικά μήκη στη Σελήνη, είτε χρησιμοποιώντας τα αντίστοιχα μεγέθη στη φωτογραφία. Η πρώτη μέτρηση δεν είναι είναι δυνατή, αλλά η δεύτερη είναι εύκολη. Για την κορυφή Α από την εικόνα 1, οι τιμές στην αρχική φωτογραφία είναι 30 mm και 2 mm, που δίνουν d=15. Αντικαθιστώντας, d=15 και r=1736 στον τύπο για το Η παίρνουμε για το ύψος της κορυφής Α, Η=3,85 km.

Αν και πρόκειται για μια χοντρική εκτίμηση, η μέθοδος του Γαλιλαίου λειτουργεί και είναι ένα εξαιρετικό παράδειγμα που μας δείχνει την δύναμη των μαθηματικών. Μια απλή αστρονομική παρατήρηση – η παρουσία μικροσκοπικών φωτεινών σημείων στη σκοτεινή πλευρά της Σελήνης – όταν ιδωθεί στο σωστό μαθηματικό πλαίσιο δίνει την απάντηση σε ένα πρόβλημα που φαίνεται αδύνατον να λυθεί: Ποιο είναι το ύψος ενός βουνού στη Σελήνη;

Πηγή: arxiv.org

Κατηγορίες:

Φυσική & Φιλοσοφία

Tags: σελήνη, φεγγάρι, βουνό, μέτρηση, υψόμετρο

Διαστημικά Νέα: Εσχάτη Θούλη & η Κίνα στη «σκοτεινή» πλευρά της Σελήνης!

3 Ιανουαρίου 2019

| 0 ΣΧΟΛΙΑ

Η «σκοτεινή» πλευρά του φεγγαριού, σε φωτογραφία από την κινεζική αποστολή

Η Εσχάτη και η Θούλη, το απώτατο γνωστό διαστημικό σώμα ως τώρα

Οι επιστήμονες της αποστολής του σκάφους New Horizons (Νέοι Ορίζοντες) της Αμερικανικής Διαστημικής Υπηρεσίας (NASA) έδωσαν στη δημοσιότητα νέες καλύτερης ανάλυσης φωτογραφίες της Εσχάτης Θούλης, του πιο μακρινού διαστημικού σώματος που έχει ποτέ εξερευνηθεί, οι οποίες αποκαλύπτουν ότι έχει σχήμα χιονάνθρωπου, διαφορετικό από οτιδήποτε άλλο έχει βρεθεί μέχρι σήμερα.

Η Εσχάτη και η Θούλη όπως φωτογραφήθηκαν από το New Horizons

To New Horizons, πέρασε κοντά στο Ultima Thule (ελληνιστί Εσχάτη Θούλη) καταφέρνοντας κάτι ιστορικό, καθώς πρόκειται για το πιο μακρινό σώμα που έχει ποτέ επισκεφθεί μια διαστημοσυσκευή, σε απόσταση περίπου 6,5 δισεκατομμυρίων χιλιομέτρων από τη Γη, στην παγωμένη Ζώνη Κάιπερ

Οι νέες φωτογραφίες από απόσταση περίπου 27.000 χιλιομέτρων δείχνουν ότι η Εσχάτη Θούλη (επισήμως γνωστή ως «2014 MU69») αποτελείται από δύο ανισομεγέθεις ακανόνιστες σφαίρες κολλημένες μεταξύ τους, δημιουργώντας ένα ενιαίο σώμα συνολικής διαμέτρου 33 χιλιομέτρων, δηλαδή, όσο το μέγεθος μιας πόλης.

Οι επιστήμονες εκμεταλλεύθηκαν το διπλό όνομα του σώματος για να βαφτίσουν τη μία σφαίρα Εσχάτη (διαμέτρου 19 χιλιομέτρων) και την άλλη Θούλη (14 χιλιομέτρων). Το όλο σώμα είναι πολύ σκούρο, καθώς η μεγαλύτερη σφαίρα αντανακλά μόνο το 13% του φωτός που πέφτει πάνω της, ενώ η μικρότερη ποσοστό 6%.

Ενδιαφέρον παρουσιάζει και η ιστορία του ονόματος του συμπλέγματος:

Η αρχαία Θούλη είναι νησί που αναφέρει ο αρχαίος Έλληνας ερευνητής Πυθέας ο Μασσαλιώτης τον 4ο αιώνα π.Χ.

Το 325 π.Χ. περίπου ταξίδεψε από τη νότια Ισπανία στη Μεγάλη Βρετανία. Σύμφωνα με τα γραπτά του, η Θούλη βρίσκεται στον ακραίο βορρά, έξι μέρες βόρεια της Βρετανίας. Για τον λόγο αυτό, το όνομα της Θούλης συμβολίζει από την εποχή της αρχαιότητας την πιο βόρεια άκρη του κόσμου (λατ. ultima thule, από όπου προέκυψε και η ονομασία του σώματος).

Από τα βιβλία του Πυθέα περί Ωκεανού και Γης σώζονται μόνο αποσπάσματα. Συνεπώς υπάρχουν διάφορες υποθέσεις σχετικά με το ποια ήταν η Θούλη. Μάλλον πρόκειται για την Ισλανδία, τη Νορβηγία, τις Νήσους Φερόες ή τις Νήσους Σέτλαντ. Ο Πυθέας αναφέρει ότι ήταν μία γεωργική χώρα, όπου η μεγαλύτερη ημέρα διαρκεί 20 (ισημερινές) ώρες. Οι εκεί κάτοικοι τρέφονταν με φρούτα και παρασκεύαζαν ένα ποτό από σιτάρι και μέλι.

Οι πρώτες έγχρωμες φωτογραφίες επίσης δείχνουν ότι η Έσχατη Θούλη έχει κοκκινωπή απόχρωση, πιθανώς επειδή η ισχυρή κοσμική ακτινοβολία έχει δώσει μια εξωτική απόχρωση στους επιφανειακούς πάγους της (κάτι ανάλογο συμβαίνει σε τμήματα του Πλούτωνα).

Κατά πάσα πιθανότητα, σύμφωνα με τις εκτιμήσεις των επιστημόνων, οι δύο σφαίρες ενώθηκαν με μη βίαιο τρόπο στην αρχική φάση σχηματισμού του ηλιακού μας συστήματος πριν από περίπου 4,5 δισεκατομμύρια χρόνια, κινούμενες η μία προς την άλλη με χαμηλή ταχύτητα δύο έως τριών χιλιομέτρων την ώρα.

Ακόμη υψηλότερης ανάλυσης φωτογραφίες και άλλα δεδομένα που έχει συλλέξει με τα όργανά του το σκάφος θα συνεχίσουν να φθάνουν στη Γη τις επόμενες μέρες, εβδομάδες και μήνες έως το 2020. Μέχρι τώρα ούτε το 1% των δεδομένων αυτών δεν έχει έλθει στη Γη.

Η πρώτη καλής ανάλυσης φωτογραφία, από απόσταση μόνο 3.500 χιλιομέτρων, αναμένεται να φτάσει μέσα στο Φεβρουάριο.

Η Κίνα στην «σκοτεινή» πλευρά του φεγγαριού

Το σκάφος, που είχε εκτοξευθεί στις 7 Δεκεμβρίου με ένα πύραυλο Long March-3B, με σκοπό να μελετήσει τη σκοτεινή πλευρά της Σελήνης, η οποία είναι μόνιμα αόρατη από τη Γη, περιλαμβάνει μια στατική άκατο και ένα μικρό ρόβερ, ενώ πολλά από τα επιστημονικά όργανα του είναι ευρωπαϊκής κατασκευής.

Μέχρι σήμερα, όλες οι αμερικανικές και σοβιετικές-ρωσικές αποστολές είχαν γίνει στη «μπροστινή», φωτεινή πλευρά. Ποτέ έως τώρα κάποιο σκάφος ή αστροναύτης δεν είχε επιχειρήσει να «πατήσει» τη λεγόμενη σκοτεινή πλευρά, τη «Luna Incognita», η οποία στην πραγματικότητα δεν είναι σκοτεινή, αφού δέχεται το φως του Ήλιου, όταν το φεγγάρι βρίσκεται ανάμεσα στη Γη και στο μητρικό άστρο μας. Η μόνη εξαίρεση ήταν το 1962, όταν το σκάφος Ranger 4 της NASA είχε συντριβεί στην «πίσω» πλευρά της Σελήνης.

Οι παρατηρήσεις από ψηλά της σκοτεινής πλευράς του φεγγαριού, τόσο από δορυφόρους, όσο και από τους αστροναύτες μέσα στις διαστημικές ακάτους, έχουν αποκαλύψει ότι -για άγνωστο λόγο- διαθέτει παχύτερο και μεγαλύτερης ηλικίας φλοιό, καθώς επίσης περισσότερους και βαθύτερους κρατήρες απ' ό,τι η φωτεινή πλευρά. Αποτελεί ακόμη μυστήριο για τους επιστήμονες γιατί τα δύο «πρόσωπα» της Σελήνης έχουν αυτές τις διαφορές.

Η Εθνική Υπηρεσία Διαστήματος της Κίνας (CNSA) ξεκίνησε το διαστημικό πρόγραμμά της για τη Σελήνη με καθυστέρηση περίπου τριών δεκαετιών, αφότου οι ΗΠΑ και η Σοβιετική Ένωση είχαν πλέον σταματήσει τις δικές τους αποστολές («Απόλλων» και «Λούνα» αντίστοιχα).

Το πρώτο κινεζικό σκάφος Chang'e-1 (είναι το όνομα της αρχαίας κινεζικής θεότητας του φεγγαριού) εκτοξεύθηκε το 2007 και αφού τέθηκε σε τροχιά και χαρτογράφησε τη Σελήνη, συνετρίβη πάνω της το 2009. Ακολούθησε τοChang'e-2 το 2010, το οποίο επίσης τέθηκε σε τροχιά γύρω από το δορυφόρο και μετά στάλθηκε στα βάθη του διαστήματος.

Το 2013, το Chang'e-3 υπήρξε το πρώτο σκάφος που προσεληνώθηκε μετά το σοβιετικό Λούνα-24 το 1976. Για πρώτη φορά μάλιστα ένα μικρό κινεζικό ρόβερ, το Yutu, ήταν εφοδιασμένο με ένα ραντάρ που μπόρεσε να μελετήσει όχι μόνο την επιφάνεια, αλλά και το υπέδαφος του φεγγαριού.

Το Chang'e-4, που έχει σχεδιασθεί κατά τα πρότυπα του προδρόμου του, θα βασίζεται για τις επικοινωνίες του με τη Γη στον κινεζικό δορυφόρο αναμετάδοσης Queqiao που διαθέτει μια παραβολική αντένα 4,2 μέτρων. Εκτοξεύθηκε φέτος το Μάιο και βρίσκεται στην κατάλληλη τροχιά, σε απόσταση 64.000 χιλιομέτρων από την πίσω πλευρά του φεγγαριού, ώστε να βλέπει ταυτόχρονα τόσο τη σκοτεινή πλευρά της Σελήνης, όσο και τον πλανήτη μας.

Το Chang'e-4, που περιλαμβάνει μια άκατο προσελήνωσης βάρους 3,6 μετρικών τόνων και το μικρό ρόβερ Yutu, βάρους 140 κιλών, προσεληνώθηκε στον διαμέτρου 180 χιλιομέτρων κρατήρα Φον Κάρμαν μέσα στην τεράστια λεκάνη Νοτίου Πόλου-Άιτκεν, η οποία πιθανόν έχει σχηματισθεί μετά την πρόσκρουση ενός γιγάντιου αστεροειδούς. Η εν λόγω λεκάνη, διαμέτρου 2.500 χιλιομέτρων και βάθους 12 χιλιομέτρων, είναι η μεγαλύτερη, βαθύτερη και παλαιότερη λεκάνη πρόσκρουσης στο φεγγάρι.

Το ραντάρ του ρόβερ θα μπορεί να «δει» σε βάθος έως 100 μέτρων κάτω από τη σεληνιακή επιφάνεια. Το σκάφος διαθέτει επίσης τρεις κάμερες και μια σειρά από επιστημονικά όργανα (ορισμένα ευρωπαϊκής κατασκευής), όπως ένα αναλυτή σεληνιακής σκόνης, ένα αναλυτή ηλεκτρικού πεδίου, ένα σεληνιακό σεισμογράφο κ.α.

Ακόμη, θα μεταφέρει ένα πείραμα 28 κινεζικών πανεπιστημίων, συγκεκριμένα μια μίνι «σεληνιακή βιόσφαιρα», μια αλουμινένια σφαίρα βάρους τριών κιλών, που περιέχει νερό, θρεπτικά συστατικά και αέρα και μέσα στην οποία θα επιχειρηθεί να φυτρώσουν σπόροι από πατάτες και άλλα φυτά. Το πείραμα θα αποτελέσει «πιλότο» για τα μελλοντικά σχέδια δημιουργίας κινεζικής σεληνιακής βάσης και τροφοδοσίας της με αγροτικά προϊόντα σεληνιακής καλλιέργειας.

Το κινεζικό σεληνιακό πρόγραμμα θα συνεχισθεί με την αποστολή Chang'e-5, τη δεύτερη στη «φωτεινή» πλευρά, που θα φέρει δείγματα βάρους έως δύο κιλών από το έδαφος και το υπέδαφος του φεγγαριού και η οποία προγραμματίζεται να εκτοξευθεί προς το τέλος του 2019. Η επόμενη αποστολή Chang'e 6 θα φέρει ένα ακόμη μεγαλύτερο δείγμα.

Απώτερος στόχος της Κίνας είναι να στείλει αστροναύτες στο φεγγάρι έως το τέλος της δεκαετίας του 2030. Η χώρα δεν έχει μόνο επιστημονικό ενδιαφέρον για τη Σελήνη, αλλά τη θεωρεί επίσης σημαντικό στρατηγικό παράγοντα στο πλαίσιο της ευρύτερης στρατηγικής να γίνει η νέα παγκόσμια υπερδύναμη.

Σε κάθε περίπτωση είναι σαφές ότι έχει ανανεωθεί το διεθνές ενδιαφέρον για τη Σελήνη, με ένα τρόπο που φέρνει στο νου την ψυχροπολεμική κούρσα ανταγωνισμού μεταξύ ΗΠΑ-ΕΣΣΔ. Η NASA - έπειτα από εντολή του προέδρου Ντόναλντ Τραμπ - έχει πλέον αρχίσει να θέτει σε εφαρμογή, σε συνεργασία με αμερικανικές εταιρίες, ένα φιλόδοξο πρόγραμμα που περιλαμβάνει μέσα στην επόμενη δεκαετία τη δημιουργία επανδρωμένου τροχιακού σταθμού γύρω από τη Σελήνη, αλλά και μιας πιο μόνιμης παρουσίας αστροναυτών πάνω στο φεγγάρι.

Η Ευρώπη, η Ρωσία, η Ινδία (εκτόξευση της σεληνιακής ακάτου Chandrayaan 2 στις αρχές του 2019) και η Ιαπωνία έχουν επίσης σχέδια για το φεγγάρι, είτε μόνες τους, είτε στο πλαίσιο διεθνούς συνεργασίας. Το μεγάλο ερώτημα όσον αφορά τη «σεληνιακή γεωπολιτική» είναι κατά πόσο θα υπάρξει διαστημικός ανταγωνισμός ή συνεργασία μεταξύ των χωρών.

Πηγές: cnn.gr, news247.gr

Κατηγορίες:

Νέα

Tags: Εσχάτη Θούλη, Ultima Thule, Προσελήνωση, φεγγάρι, Κίνα

ΑΡΘΡΑ

ΣΧΟΛΙΑ

φεγγάρι (5 άρθρα)

Γιατί αυξήθηκε η διάρκεια της ημέρας κατά 30 λεπτά από την εποχή των δεινοσαύρων;

Γιατί δεν είναι όλοι βέβαιοι ότι ο άνθρωπος πάτησε στη Σελήνη;

Οι ήχοι πλανητών και λοιπών ουρανίων σωμάτων, όπως τους κατέγραψε η NASA!

Η Φυσική των διαστημικών ήχων

Πώς ακούγονται πλανήτες και άλλα ουράνια σώματα;

Πώς μετράμε το ύψος ενός βουνού της Σελήνης;

Διαστημικά Νέα: Εσχάτη Θούλη & η Κίνα στη «σκοτεινή» πλευρά της Σελήνης!