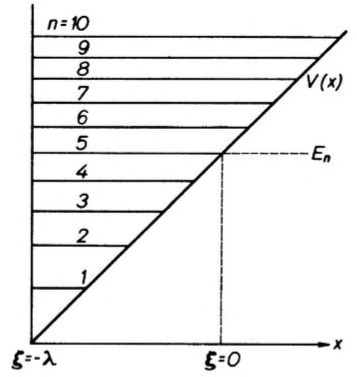
Ένα από τα απλούστερα και σημαντικότερα προβλήματα της κλασικής φυσικής, είναι η μελέτη της κίνησης μιας μπάλας μάζας m που αφήνεται να πέσει ελεύθερα από ύψος H και ανακλάται ελαστικά από το οριζόντιο επίπεδο έδαφος.
Aν g είναι η σταθερή επιτάχυνση της βαρύτητας (ή η ένταση του ομογενούς βαρυτικού πεδίου) και δεν υπάρχει αντίσταση του αέρα, τότε η συνολική της μηχανική ενέργεια παραμένει συνεχώς σταθερή: . Όταν η μπάλα απέχει απόσταση x από το έδαφος, έχει ταχύτητα:
. Η συνολική ενέργεια της μπορεί να πάρει οποιαδήποτε τιμή στο συνεχές διάστημα τιμών
για
και προφανώς, η ελάχιστη τιμή της σ’ αυτό το συνεχές εύρος είναι Ε=0, όταν H=0.
Όμως, αν αντί για ένα μακροσκοπικό αντικείμενο όπως η μπάλα, πέφτει ελεύθερα και αναπηδά ελαστικά ένα μικροσκοπικό σωματίδιο, τότε η συμπεριφορά του θα είναι κβαντομηχανική. Η ενέργεια του σωματιδίου θα παίρνει διακριτές τιμές και η ελάχιστη τιμή της θα είναι διάφορη του μηδενός.
Στη συνέχεια θα εξετάσουμε την ελεύθερη πτώση ενός σωματιδίου στο πλαίσιο της κβαντικής φυσικής.
Ένας γρήγορος τρόπος να εκτιμήσουμε την τάξη μεγέθους της ελάχιστης ενέργειας (της ενέργειας στην θεμελιώδη κατάσταση) είναι να εφαρμόσουμε την αρχή της αβεβαιότητας
. Η αβεβαιότητα στη θέση θα είναι της τάξης
, ενώ η αβεβαιότητα στην ορμή
, οπότε
. Λύνοντας ως προς την ενέργεια παίρνουμε:
Η πλήρης κβαντομηχανική περιγραφή θα προκύψει από την μονοδιάστατη εξίσωση Schrödinger για ένα σωματίδιο με δυναμική ενέργεια U(x)=mgx :
ή
Αναζητούμε λύση της εξίσωσης για και οριακές συνθήκες
και
.
For old times’ sake, ακολουθούμε τον τρόπο επίλυσης που περιγράφεται στο βιβλίο του Siegfried Flügge, «Practical Quantum Mechanics»: Θέτoντας και
, η εξίσωση Schrödinger απλοποιείται στην απλούστερη μορφή της διαφορικής εξίσωσης Airy:
, με οριακές συνθήκες:
και
. Παρατηρείστε ότι η τιμή ξ=0 αντιστοιχεί στην
και ότι η κίνηση του σωματιδίου, όταν εξετάζεται κλασικά, περιορίζεται στο εύρος
ή
.
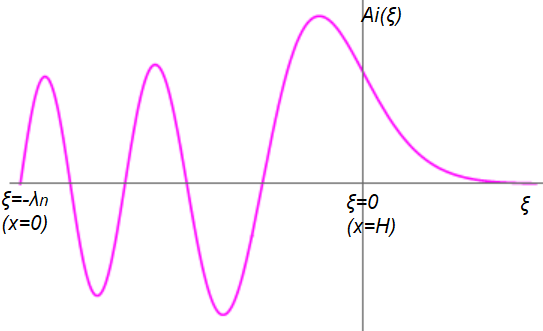
H γενική λύση της εξίσωσης είναι ένας γραμμικός συνδυασμός των συναρτήσεων Airy: (1)
Δεδομένου ότι , προκύπτει ότι c2=0 και η εξ. (1) γίνεται
. Από την οριακή συνθήκη (για
ή
) θα έχουμε:
, η οποία επαληθεύεται για τις διακριτές τιμές
:
, κ.ο.κ.
Από τις σχέσεις , προκύπτει ότι η ενέργεια παίρνει τις τιμές:
, με την ενέργεια της θεμελιώδους κατάστασης να είναι:
.
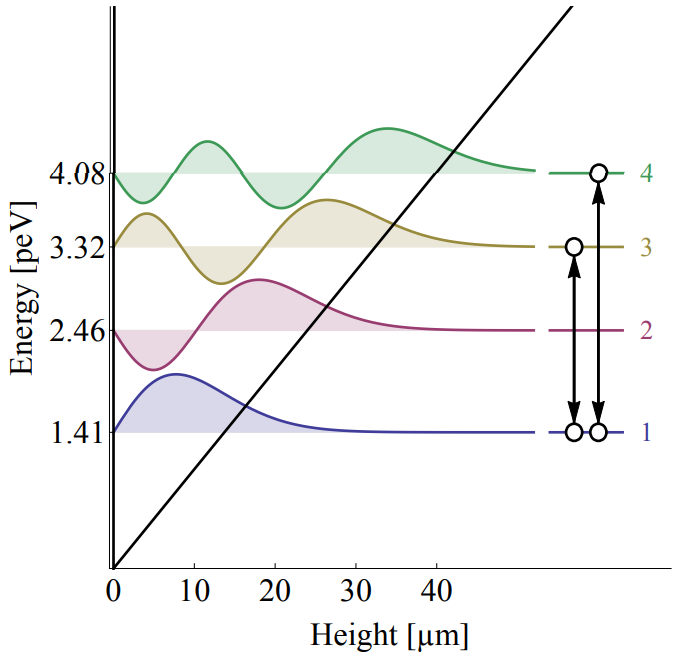
Μπορεί όλα τα παραπάνω να φαίνονται πολύ θεωρητικά, όμως η κβαντομηχανική ελεύθερη πτώση σωματιδίου που ανακλάται ελαστικά σε ακλόνητο οριζόντιο επίπεδο, έχει πραγματοποιηθεί πειραματικά με υπερ-ψυχρά νετρόνια, με ταχύτητες περίπου 8 m/s. Οι πέντε πρώτες ιδιοκαταστάσεις, με τις αντίστοιχες ιδιο-ενέργειες του υπερ-ψυχρού νετρονίου που πέφτει ελεύθερα και αναπηδά ελαστικά, φαίνονται στο παρακάτω διάγραμμα, από την εργασία των Cronenberg et al, ‘A Gravity of Earth Measurement with a qBOUNCE Experiment‘: