… ποιός θα αποφασίσει τι θα κάνουμε στη συνέχεια; Πολλοί επιστήμονες ανησυχούν ότι οι άνθρωποι θα αντιδρούσαν «σαν ακέφαλα κοτόπουλα»
Η επιστημονική φαντασία περιέγραψε αυτή τη στιγμή χιλιάδες φορές. Καθώς οι αστρονόμοι χτενίζουν το σύμπαν με τα ισχυρά τηλεσκόπια τους, εντοπίζουν κάτι που τους κόβει την ανάσα. Ένα αδύναμο αλλά επίμονο σήμα: ένα μήνυμα από έναν προηγμένο πολιτισμό.
Θα ήταν ένα συγκλονιστικό γεγονός για την ανθρωπότητα, κάτι για το οποίο δεν είναι προετοιμασμένα τα έθνη του κόσμου. «Δείτε το χάος που δημιουργήθηκε όταν χτύπησε ο Covid. Θα ήμαστε σαν ακέφαλα κοτόπουλα», λέει ο Δρ John Elliott, γλωσσολόγος από το Πανεπιστήμιο του St Andrews. «Δεν έχουμε την πολυτέλεια να είμαστε κακώς προετοιμασμένοι, επιστημονικά, κοινωνικά και πολιτικά χωρίς σχέδιο, για ένα γεγονός που θα μπορούσε να συμβεί ανά πάσα στιγμή, για το οποίο δεν έχουμε την πολυτέλεια κακής διαχείρισης»
Αυτή η ειλικρινής παραδοχή της έλλειψης ετοιμότητας για επαφή με εξωγήινο πολιτισμό οδήγησε στη δημιουργία του κόμβου μετα-ανίχνευσης Seti (Αναζήτηση για Εξωγήινη Νοημοσύνη) στο St Andrews.
Μέσα στους επόμενους μήνες, ο Elliott στοχεύει να συγκροτήσει μια ομάδα ερευνητών που θα αναλάβει τη δουλειά της προετοιμασίας σχετικά με την ανάλυση μυστηριωδών σημάτων
και της επεξεργασίας κάθε τρόπου με τον οποίο θάπρεπε να αντιδράσουμε σε τέτοιου είδους σήματα. Χρειαζόμαστε στρατηγικές και σενάρια για να καταλάβουμε τι πρέπει να κάνουμε και πώς να το κάνουμε. Είναι σαν το σύνθημα των προσκόπων: έσο έτοιμος.
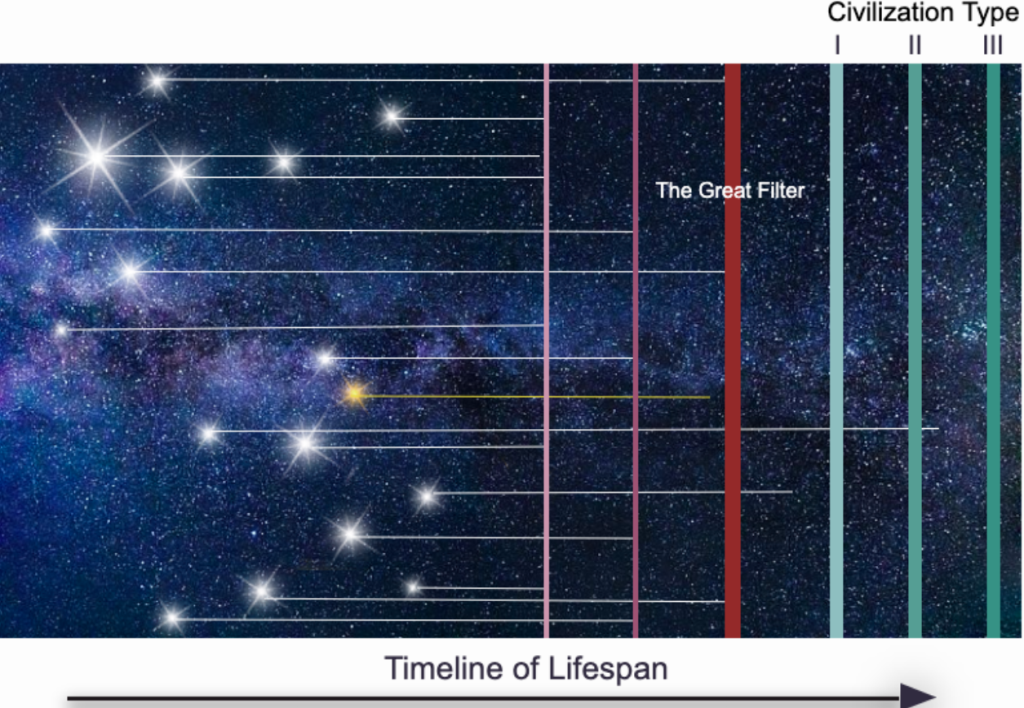
Οι εξελίξεις των τελευταίων 30 ετών έχουν αυξήσει τον ενθουσιασμό στην αναζήτηση εξωγήινων πολιτισμών. Από το 1992, όταν οι αστρονόμοι επιβεβαίωσαν για πρώτη φορά την ύπαρξη ενός πλανήτη πέρα από το ηλιακό μας σύστημα, έχουν εντοπιστεί περισσότεροι από 5.000 εξωπλανήτες. Οι επιστήμονες υποπτεύονται τώρα ότι τα περισσότερα από τα 300 δισεκατομμύρια άστρα στον Γαλαξία μας φιλοξενούν τη δική τους οικογένεια πλανητών.
Ωστόσο, η αφθονία των εξωπλανητών και η υποψία ότι τουλάχιστον ορισμένοι είναι κατοικήσιμοι, είναι μόνο ένα μέρος της ιστορίας. Πολύ πιο ισχυρά τηλεσκόπια συμμετέχουν στην έρευνα, ή θα το κάνουν σύντομα, σαρώνοντας μεγάλες περιοχές του ουρανού για να τις ‘κρυφακούσουν’ οι αστρονόμοι.
Οι ερευνητές του Seti έχουν ήδη κάποιες κατευθυντήριες γραμμές για το πώς να συμπεριφερθούν όταν εντοπίσουν ένα διαστρικό μήνυμα από έναν προηγμένο πολιτισμό. Μια ανακοίνωση του 2010 από τη Διεθνή Ακαδημία Αστροναυτικής παροτρύνει όσους εντοπίζουν μυστηριώδη σήματα να αποκλείσουν πρώτα τις πιθανές μη εξωγήινες πηγές. Αν υπάρξει ομοφωνία ότι το σήμα είναι πράγματι εξωγήινο, οι ερευνητές θα πρέπει να ενημερώσουν το κοινό και τον γενικό γραμματέα του ΟΗΕ.
Αλλά υπάρχουν ελάχιστες οδηγίες για το τι πρέπει να γίνει στη συνέχεια. Πώς πρέπει να μελετηθεί το μήνυμα; Πρέπει να δημοσιευθεί πριν αποκρυπτογραφηθεί; Θα το επέτρεπαν οι κυβερνήσεις; Πρέπει να απαντήσει η ανθρωπότητα; Αν ναι, ποιος αποφασίζει τι θα ανταπαντήσουμε;
«Μετά την αρχική ανακοίνωση, θα εξετάζαμε τον κοινωνικό αντίκτυπο, τη διασπορά πληροφοριών, τα μέσα ενημέρωσης, τον αντίκτυπο στις θρησκείες και τις διάφορες ιδεολογίες, πιθανή παραπληροφόρηση, ποιες αναλυτικές ικανότητες θα χρειαστούμε και πολλά άλλα: να έχουμε έτοιμες στρατηγικές, να είμαστε διαφανείς με όλα όσα έχουμε ανακαλύψει – τι ξέρουμε και τι δεν ξέρουμε», υποστηρίζει ο Elliott.
Ενώ μεμονωμένοι επιστήμονες και αρκετοί οργανισμοί έχουν εξετάσει τον καλύτερο τρόπο διαχείρισης της πρώτης επαφής, ο Elliott πιστεύει ότι η απαιτούμενη τεχνογνωσία είναι κατακερματισμένη. Ο κόμβος μετα-ανίχνευσης Seti στο St Andrews θα συγκεντρώσει τα απαραίτητα μυαλά για να καταρτίσει ένα σχέδιο «για όποιο σενάριο κι αν συναντήσουμε… ή τουλάχιστον για όλα αυτά που μπορούμε να σκεφτούμε εμείς – η ανθρωπότητα»
Ένας άλλος σημαντικός στόχος είναι η ανάληψη επίσημης δέσμευσης από τα Ηνωμένα Έθνη, ίσως το μόνο παγκόσμιο όργανο με την επιρροή (;) να συντονίσει τον χειρισμό ενός μηνύματος από τη Γη. Οι τεράστιες αποστάσεις μεταξύ των άστρων σημαίνουν ότι οι συνομιλίες μπορεί να έχουν τέτοια διάρκεια που θα περιλαμβάνει πολλές ανθρώπινες γενεές. Κι αυτό σημαίνει ότι ο εξωγήινος πολιτισμός δεν θα έχει εξαφανιστεί στο χρονικό διάστημα που χρειάστηκε το μήνυμα να φτάσει σε μάς.
Όμως, στ’ αλήθεια θα μπορέσουμε να συνομιλήσουμε με εξωγήινους όταν μετά βίας μπορούμε να επικοινωνήσουμε με πλάσματα στον δικό μας πλανήτη; Ο Elliott ελπίζει ότι οι προηγμένοι πολιτισμοί θα ξεκινήσουν οποιοδήποτε μήνυμα με έναν γλωσσικό οδηγό. Αλλά ακόμα κι αν ένα σήμα δεν είναι αποκρυπτογραφημένο, οι ερευνητές θα μπορούσαν να αντλήσουν πληροφορίες σχετικά με την ευφυΐα του αποστολέα από την πολυπλοκότητα της δομής του.
Η προοπτική αποστολής οποιασδήποτε απάντησης έχει προκαλέσει κριτική από ορισμένους κύκλους. Ο Στίβεν Χόκινγκ, ο κοσμολόγος του Κέμπριτζ, προειδοποίησε το 2016 ότι η πρώτη επαφή της ανθρωπότητας με έναν προηγμένο πολιτισμό θα μπορούσε να ισοδυναμεί με αυτό που συνέβη όταν οι ιθαγενείς της Αμερικής αντιμετώπισαν τον Χριστόφορο Κολόμβο, κάτι που «δεν πήγε τόσο καλά».
Ο Michio Kaku, καθηγητής θεωρητικής φυσικής στο City College της Νέας Υόρκης, είπε ότι η προσέγγιση με εξωγήινους «θα ήταν το μεγαλύτερο λάθος στην ανθρώπινη ιστορία».
Ωστόσο, ο Elliott είναι πιο αισιόδοξος. Πιστεύει ότι θα ήταν κρίμα οι προηγμένοι πολιτισμοί να παραμένουν απομονωμένοι, χωρίς να κάνουν προσπάθειες επικοινωνίας. «Αν υπάρχει μια άλλη νοημοσύνη εκεί έξω -που όλες οι ενδείξεις δείχνουν ότι πρέπει να υπάρχει-, αν έχουμε την ευκαιρία, δεν νομίζω ότι πρέπει να τη χάσουμε».
Ο αστροβιολόγος Lewis Dartnell στο Πανεπιστήμιο του Westminster, δήλωσε ότι ο νέος κόμβος στο St Andrews είναι ένα σημαντικό βήμα για την ευαισθητοποίηση σχετικά με το πόσο ελάχιστα προετοιμασμένοι είμαστε αυτήν τη στιγμή, για την ανίχνευση ενός σήματος από εξωγήινο πολιτισμό. Και προσθέτει ότι οποιοσδήποτε νοήμων εξωγήινος πολιτισμός είναι πιθανό να βρίσκεται εκατοντάδες, αν όχι χιλιάδες έτη φωτός μακριά, πράγμα που σημαίνει ότι ο χρόνος επικοινωνίας θα είναι στην κλίμακα πολλών αιώνων. Ακόμα κι αν λαμβάναμε ένα σήμα αύριο, θα είχαμε άφθονο χρόνο για να συγκεντρώσουμε μια διεθνή ομάδα ειδικών επιστημόνων που θα προσπαθήσουν να αποκρυπτογραφήσουν το νόημα του μηνύματος και να εξετάσουν προσεκτικά για το αν ή πώς θα έπρεπε να αντιδράσει η Γη.
Το μεγαλύτερο μέλημα είναι να καθιερωθεί κάποια μορφή διεθνούς συμφωνίας για να αποτρέψει ικανά άτομα ή ιδιωτικές εταιρείες να ανταποκριθούν ανεξάρτητα – προτού διαμορφωθεί συναίνεση για το αν είναι ασφαλές να απαντήσουμε ή όχι και τι θα θέλαμε να πούμε ως ανθρώπινος πολιτισμός.
Πηγή