Φυσική & Φιλοσοφία (201 άρθρα)

Η είδηση δεν είναι ότι το διαστημικό τηλεσκόπιο της ESA, Cheops, ανακάλυψε έναν ακόμα εξωπλανήτη, τον WASP-103b, αλλά το ότι ο εν λόγω εξωπλανήτης δεν είναι σφαιρικός και μοιάζει με μπάλα του ράγκμπι. Και είναι η πρώτη φορά που εντοπίζεται ένας τέτοιος παραμορφωμένος εξωπλανήτης.

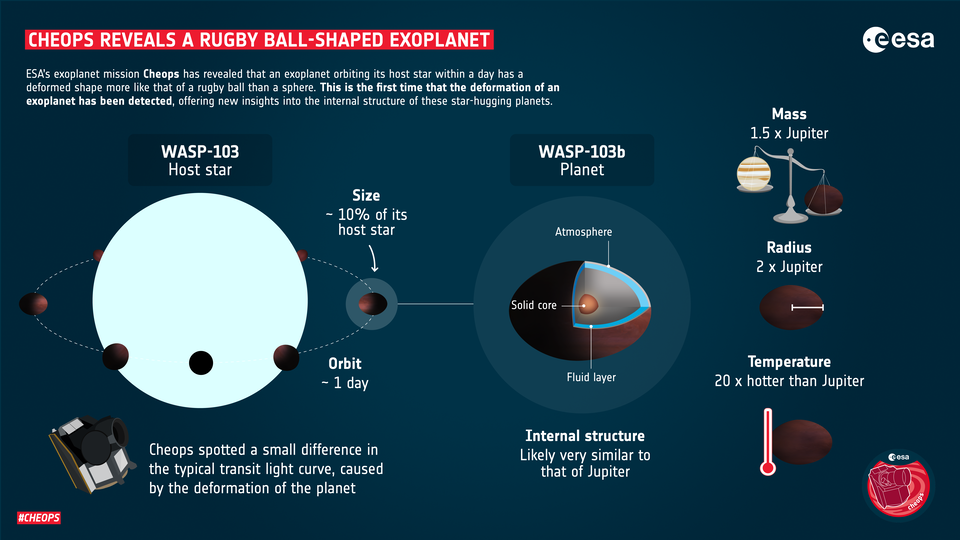
O εξωπλανήτης WASP-103b ολοκληρώνει μια περιφορά γύρω από το άστρο του μέσα σε 24 ώρες και κινείται πολύ κοντά σ’ αυτό, διαγράφοντας τροχιά ακτίνας περίπου 0,02 αστρονομικές μονάδες. Γι αυτό οι αστρονόμοι περίμεναν ότι η τροχιά σε μια τόσο κοντινή απόσταση θα προκαλούσε ισχυρές παλιρροϊκές δυνάμεις, αλλά δεν ήταν σε θέση να τις μετρήσουν. Χρησιμοποιώντας τα νέα δεδομένα από το διαστημικό τηλεσκόπιο Cheops, σε συνδυασμό με δεδομένα που είχαν ήδη ληφθεί από τα διαστημικά τηλεσκόπια Hubble και Spitzer, κατάφεραν να διαπιστώσουν την παραμόρφωση εξαιτίας των παλιρροϊκών δυνάμεων του εξωπλανήτη WASP-103b στο σχήμα μιας μπάλας του ράγκμπι.

Οι παλίρροιες στην Γη οφείλονται στην βαρυτική αλληλεπίδραση της Γης με την Σελήνη που περιφέρεται γύρω μας. Κι ο Ήλιος έχει επίσης μια μικρή αλλά σημαντική επίδραση στις παλίρροιες, όμως είναι πολύ μακριά από τη Γη για να προκαλέσει μεγάλες παραμορφώσεις στον πλανήτη μας. Δεν μπορούμε να πούμε το ίδιο και για τον WASP-103b, που περιφέρεται πολύ κοντά στο άστρο του.

Η αντίσταση ενός υλικού στην παραμόρφωση εξαρτάται από τη σύνθεσή του. Για παράδειγμα, οι παλιρροϊκές δυνάμεις στην Γη λόγω Σελήνης και Ήλιου, προκαλούν την ‘υδατική παραμόρφωση’, δηλαδή τις παλίρροιες, αλλά δεν καταφέρνουν να παραμορφώσουν σημαντικά το βραχώδες τμήμα της.

Οι αστροφυσικοί συσχετίζουν την παλλιρροϊκή παραμόρφωση με τον αριθμό Love. Όσο μεγαλύτερος είναι ο αριθμός αυτός, τόσο πιο παραμορφωμένος είναι o πλανήτης. Ο αριθμός Love του WASP-103b είναι περίπου ίδιος με τον αντίστοιχο του του Δία, κι αυτό δείχνει ότι μάλλον έχουν παρόμοια εσωτερική δομή, παρά το γεγονός ότι ο WASP-103b έχει διπλάσια ακτίνα. Οι ερευνητές θα επιχειρήσουν την διερεύνηση των λεπτομερειών της εσωτερικής του δομής του με μελλοντικές παρατηρήσεις, ώστε να κατανοήσουν γιατί είναι τόσο παραμορφωμένος. Σημαντικό ρόλο στην ερμηνεία θα παίξει και ο προσδιορισμός του μεγέθους του πυρήνα του.

Δεδομένου ότι η αβεβαιότητα στην τιμή του αριθμού Love είναι προς το παρόν αρκετά μεγάλη, απαιτούνται επιπλέον παρατηρήσεις με τα διαστημικά τηλεσκόπια Cheops και James Webb. Η εξαιρετικά υψηλή ακρίβεια του Webb θα βελτιώσει τις μετρήσεις της παλιρροιακής παραμόρφωσης των εξωπλανητών, επιτρέποντας μια καλύτερη σύγκρισή τους με τους πλανήτες-γίγαντες του ηλιακού μας συστήματος.

Όμως υπάρχει άλλο ένα μυστήριο που περιβάλλει τον WASP-103b. Οι παλιρροϊκές αλληλεπιδράσεις μεταξύ άστρου και του συγκεκριμένου εξωπλανήτη έπρεπε να προκαλέσουν μείωση της τροχιακής περιόδου του και τη σταδιακή προσέγγιση στο άστρο του με τελικό αποτέλεσμα την σύγκρουσή του με αυτό. Όμως οι μετρήσεις του WASP-103b δείχνουν αντίθετα ότι η τροχιακή περίοδος ίσως να αυξάνεται και ότι ο εξωπλανήτης απομακρύνεται αργά από το άστρο του. Αυτό μπορεί να σημαίνει ότι κάτι διαφορετικό από τις παλιρροϊκές δυνάμεις είναι ο βασικός παράγοντας που επηρεάζει αυτόν τον εξωπλανήτη.

Έτσι, οι αστροφυσικοί εξέτασαν και άλλα πιθανά σενάρια. Θα μπορούσε για παράδειγμα, η δυναμική του συστήματος να επηρεάζεται από την παρουσία ενός δεύτερου άστρου ή η τροχιά του πλανήτη να είναι ελαφρώς ελλειπτική. Δεν μπόρεσαν να επιβεβαιώσουν αυτά τα σενάρια, αλλά ούτε και να τα αποκλείσουν. Για να απαντηθούν με βεβαιότητα όλα τα ερωτήματα θα απαιτηθούν επιπλέον παρατηρήσεις των διελεύσεων του WASP-103b (μπροστά από το άστρο του) από το Cheops και άλλα τηλεσκόπια.

Το σίγουρο είναι πως η ακρίβεια των παρατηρήσεων του διαστημικού τηλεσκοπίου Χέωψ (CHaracterising ExOPlanets Satellite), που έτυχε να είναι συνονόματο με έναν σκληρό και αδίστακτο Φαραώ, αποκάλυψε για πρώτη φορά το περίεργο σχήμα του WASP-103b, ανοίγοντας νέους δρόμους όσον αφορά την μελέτη εξωπλανητών.

Πηγή

Σε δημοσίευση στο περιοδικό Nature, οι φυσικοί της ερευνητικής ομάδας BASE στο CERN, περιγράφουν την ακριβέστερη σύγκριση, μέχρι τώρα, μεταξύ πρωτονίων και αντιπρωτονίων. Αναλύοντας τις μετρήσεις που πραγματοποιήθηκαν στο ‘εργοστάσιο’ αντιύλης του CERN, η ομάδα BASE μέτρησε το πηλίκο q/m (ηλεκτρικό φορτίο προς μάζα) των πρωτονίων (p) και των αντιπρωτονίων () με εκπληκτική ακρίβεια. Διαπίστωσαν ότι οι δύο λόγοι ταυτίζονται με μια πειραματική αβεβαιότητα 16 προς ένα τρισεκατομμύριο:

Σύμφωνα με το Καθιερωμένο Πρότυπο των στοιχειωδών σωματιδίων, τα σωματίδια ύλης και αντιύλης μπορεί να διαφέρουν, π.χ. στον τρόπο με τον οποίο μετατρέπονται σε άλλα σωματίδια, αλλά οι περισσότερες ιδιότητές τους, συμπεριλαμβανομένων και των μαζών τους, πρέπει να είναι πανομοιότυπες. Η εύρεση οποιασδήποτε μικρής διαφοράς μεταξύ των μαζών πρωτονίων και αντιπρωτονίων, ή μεταξύ των λόγων q/m, θα έσπαγε μια θεμελιώδη συμμετρία που ονομάζεται συμμετρία CPT και θα οδηγούσε σε νέα φυσική πέρα ​​από το Καθιερωμένο Πρότυπο. Μια τέτοια διαφορά θα μπορούσε επίσης να ρίξει φως στο γιατί το σύμπαν αποτελείται σχεδόν εξ ολοκλήρου από ύλη, παρόλο που κατά την Μέγάλη Έκρηξη προέκυψαν ίσες ποσότητες ύλης και αντιύλης. Όμως, οι διαφορές μεταξύ σωματιδίων ύλης και αντιύλης που προκύπτουν από τα πειράματα είναι τάξεις μεγέθους μικρότερες από τις τιμές που απαιτούνται για να κλονίσουν το Καθιερωμένο Πρότυπο.

Τα αρχικά CPT αναφέρονται, C: στην συζυγία φορτίου, τον μετασχηματισμό όπου ένα σωματίδιο αντικαθίσταται από το αντισωματίδιό του, P: στην ομοτιμία, η οποία συνδέεται με τον μετασχηματισμό αναστροφής του χώρου, και T: στη συμμετρία αναστροφής του χρόνου, όπου εναλλάσσονται οι χρονικές συντεταγμένες t και -t.
Oι ισχυρές και οι ηλεκτρομαγνητικές αλληλεπιδράσεις παραμένουν αναλλοίωτες κάτω από τους προαναφερθέντες μετασχηματισμούς C, P και T, ενώ οι ασθενείς αλληλεπιδράσεις παραβιάζουν μεμονωμένα και τις 3 αυτές συμμετρίες. Όμως, όταν οι μετασχηματισμοί C, P, Τ εφαρμόζονται μαζί, ως μετασχηματισμός CPT, τότε όλες οι αλληλεπιδράσεις – ασθενείς, ισχυρές και ηλεκτρομαγνητικές – παραμένουν αναλλοίωτες. Αυτό είναι το θεώρημα CPΤ και διατυπώνεται απλούστερα ως εξής: ένα σύστημα παραμένει αμετάβλητο αν τα σωματίδια αντικατασταθούν από τα κατοπτρικά συμμετρικά αντισωματίδιά τους και αντιστραφεί η ροή του χρόνου. To «αναλλοίωτο CPT» μας εγγυάται ότι ένα σωματίδιο και το αντισωματίδιό του έχουν ίσες μάζες, ίσους χρόνους ζωής, ίδιο σπιν, αλλά αντίθετους προσθετικούς κβαντικούς αριθμούς όπως το ηλεκτρικό φορτίο, η z συνιστώσα του ισοσπίν, ο κβαντικός αριθμός της παραξενιάς κ.ά.Όλα τα πειράματα που έχουν γίνει μέχρι σήμερα δείχνουν ότι δεν παραβιάζεται η συμμετρία CPT.

Για να πραγματοποιηθούν οι μετρήσεις πρωτονίων και αντιπρωτονίων, η ομάδα BASE εγκλώβισε τα αντιπρωτόνια και τα αρνητικά φορτισμένα ιόντα υδρογόνου (άτομα υδρογόνου στα οποία προστίθεται ένα επιπλέον ηλεκτρόνιο που χρησιμιμοποιώνται ως υποκατάστατα των πρωτονίων), σε μια συσκευή που ονομάζεται παγίδα Penning. Εκεί, ένα σωματίδιο ακολουθεί μια κυκλική τροχιά με συχνότητα, κοντά στη συχνότητα του κυκλότρου, η ακτίνα της οποίας εξαρτάται από την ένταση του μαγνητικού πεδίου και τον λόγο του ηλεκτρικού φορτίου προς την μάζα του σωματιδίου.

Διοχετεύοντας αντιπρωτόνια και αρνητικά φορτισμένα ιόντα υδρογόνου στην παγίδα, η ομάδα BASE συνέκρινε, κάτω από τις ίδιες συνθήκες, τον λόγο q/m (φορτίο προς μάζα) των πρωτονίων και των αντιπροτωνίων. Διαπίστωσαν ότι είναι ίσoι με ακρίβεια 16 προς 1000000000000! Αυτό το αποτέλεσμα είναι τέσσερις φορές ακριβέστερο σε σχέση με την αντίστοιχη προηγούμενη μέτρηση.

Εκτός από τη σύγκριση του λόγου q/m πρωτονίων και αντιπρωτονίων με πρωτοφανή ακρίβεια, η ομάδα BASE χρησιμοποίησε τις μετρήσεις της για να θέσει αυστηρά όρια σε θεωρίες πέρα ​​από το Καθιερωμένο Πρότυπο οι οποίες παραβιάζουν την συμμετρία CPT, καθώς και για να ελέγξει την ασθενή αρχή ισοδυναμίας. Σύμφωνα με αυτή την αρχή, διαφορετικά σώματα στο ίδιο βαρυτικό πεδίο υφίστανται την ίδια επιτάχυνση απουσία δυνάμεων τριβής. Το πείραμα BASE και οι μετρήσεις συχνότητας περιστροφής πρωτονίων και αντιπρωτονίων στο κύκλοτρο έγιναν στο βαρυτικό πεδίο στην επιφάνεια της Γης. Οποιαδήποτε διαφορά της βαρυτικής αλληλεπίδρασης των πρωτονίων με την αντίστοιχη βαρυτική αλληλεπεδρίση των αντιπρωτονίων θα οδηγούσε σε διαφορά μεταξύ των συχνοτήτων περιστροφής πρωτονίων και αντιπρωτονίων.

Oι φυσικοί του BASE δεν βρήκαν τέτοια διαφορά μέσα στα όρια του σφάλματος του πειράματος. Το σφάλμα αυτής της μέτρησης είναι συγκρίσιμο με το αντίστοιχο σφάλμα των πειραμάτων που μελετούν την απευθείας ελεύθερη πτώση των πρωτονίων στο πεδίο βαρύτητας της Γης.

Πηγή

Εκτοξεύθηκε με επιτυχία το διαστημικό τηλεσκόπιο James Webb, ο διάδοχος του παλαιότερου τηλεσκοπίου Hubble. Το James Webb είναι το μεγαλύτερο και το πιο εξελιγμένο τηλεσκόπιο που έχει ποτέ σταλεί στο διάστημα, ανοίγοντας έτσι μια νέα εποχή στην αστρονομία και στην αστροφυσική. Πρόκειται για μια αποστολή συνεργασίας της Αμερικανικής Διαστημικής Υπηρεσίας (NASA), του Ευρωπαϊκού Οργανισμού Διαστήματος (ESA) και της Καναδικής Διαστημικής Υπηρεσίας.

Η εκτόξευση έγινε με έναν ευρωπαϊκό πύραυλο Arian 5, λίγο μετά το μεσημέρι, από το ευρωπαϊκό διαστημοδρόμιο στο Κουρού της Γαλλικής Γουινέας στη βορειοανατολική Νότια Αμερική. Το κόστους 10 δισεκατομμυρίων δολαρίων τηλεσκόπιο θα τεθεί σε τροχιά γύρω από τον Ήλιο στο δεύτερο σημείο Lagrange ή L2, μένοντας σε περίπου σταθερή απόσταση 1,5 εκατομμυρίων χιλιομέτρων από τη Γη ή περίπου τέσσερις φορές πιο μακριά από τη Σελήνη. Συγκριτικά, το διαστημικό τηλεσκόπιο Hubble – που είχε εκτοξευθεί το 1990 – βρίσκεται στο ένα τρίτο αυτής της απόστασης από τον πλανήτη μας (σχεδόν 550 χιλιόμετρα).

Το James Webb αναμένεται να φτάσει στο σημείο L2 ένα μήνα μετά την εκτόξευσή του. Στη συνέχεια, θα υπάρξει μια περίοδος εγκατάστασης και προσαρμογής που θα διαρκέσει έξι μήνες. Αναμένεται να αρχίσει να συλλέγει δεδομένα και να κάνει τις πρώτες παρατηρήσεις στα μέσα του 2022.

Το τηλεσκόπιο, που κατασκευάστηκε κυρίως από την αμερικανική εταιρεία Northrop Grumman και φέρει το όνομα του επικεφαλής της NASA στη δεκαετία του 1960, είναι πολύ πιο ευαίσθητο από το Hubble και θα «βλέπει» κυρίως στο υπέρυθρο τμήμα του φάσματος, πράγμα που θα του επιτρέπει να παρατηρεί μέσα από τα νέφη σκόνης και αερίων, ενώ το Hubble λειτουργεί κυρίως στο οπτικό και υπεριώδες τμήμα του φάσματος.

Το νέο τηλεσκόπιο, που θα παρέχει βελτιωμένη υπέρυθρη ανάλυση και ευαισθησία σε σχέση με το Hubble, θα χρησιμοποιηθεί σε ένα τεράστιο εύρος ερευνών στους τομείς της αστρονομίας, της αστροφυσικής και της κοσμολογίας, από τη μελέτη της ατμόσφαιρας σχετικά κοντινών εξωπλανητών μέχρι την παρατήρηση των μακρινών πρώτων γαλαξιών.

Το James Webb έχει μάζα 6 τόνους και 6,25 φορές μεγαλύτερη συλλεκτική επιφάνεια, άρα και ευαισθησία, συγκριτικά με το Hubble. Επιπρόσθετα, έχει σημαντικά μεγαλύτερο οπτικό πεδίο, καλύπτοντας 15 φορές μεγαλύτερη περιοχή του ουρανού. Το πρωτεύον κάτοπτρό του αποτελείται από 18 εξαγωνικά τμήματα, που είναι κατασκευασμένα από επιχρυσωμένο βηρύλλιο, τα οποία ξεδιπλώνουν και προσαρμόζονται σχηματίζοντας ένα κάτοπτρο διαμέτρου 6,5 μέτρων. Το μεγαλύτερο εξάρτημα του είναι η ηλιακή ασπίδα πέντε στρωμάτων, που μειώνει την ηλιακή ακτινοβολία που φτάνει στο τηλεσκόπιο κατά ένα εκατομμύριο φορές και είναι η κύρια αιτία του μεγάλου μεγέθους του (20 επί 14 μέτρα).

1ος νόμος Kepler: Οι τροχιά ενός πλανήτη είναι έλλειψη και Ήλιος βρίσκεται στην μία εστία της έλλειψης.
2ος νόμος Kepler: Η ακτίνα που ενώνει τον Ήλιο και τον κάθε πλανήτη διαγράφει σε ίσους χρόνους ίσα εμβαδά.
3ος νόμος Kepler: Το τετράγωνο της περιόδου περιφοράς του κάθε πλανήτη είναι ανάλογο με τον κύβο του μήκους του μεγάλου ημιάξονα της έλλειψης που διαγράφει.

Στο παραπάνω σχήμα βλέπουμε έναν πλανήτη μάζας m σε τροχιά γύρω από τον Ήλιο μάζας Μ (πολύ μεγαλύτερη της m). Η ταχύτητα του πλανήτη είναι συνεχώς εφαπτόμενη στην τροχιά του και σχηματίζει γωνία φ με το διάνυσμα θέσης . Η δύναμη της βαρύτητας είναι κεντρική και η στροφορμή του πλανήτη

διατηρείται σταθερή. Έτσι, η διεύθυνση του διανύσματος της στροφορμής θα παραμένει σταθερή, οπότε η τροχιά του πλανήτη θα είναι επίπεδη (η στροφορμή έχει την ίδια κατεύθυνση με το διάνυσμα που είναι κάθετο στα και ).

Η μηχανική ενέργεια του πλανήτη

διατηρείται επίσης σταθερή. Λύνοντας την εξ. (2) ως προς την ταχύτητα και αντικαθιστώντας στην (1) παίρνουμε: , και αναδιατάσσοντας τους όρους:

H παραπάνω εξίσωση μας δείχνει πως μεταβάλλεται η γωνία της εφαπτόμενης στην τροχιά με το διάνυσμα θέσης του πλανήτη και θα μπορούσε να είναι η εξίσωση της τροχιάς του πλανήτη. Το ζητούμενο λοιπόν είναι να αποδείξουμε ότι η παραπάνω εξίσωση εκφράζει μια έλλειψη – μια εξίσωση έλλειψης που δεν συναντάμε στα βιβλία.

Άσκηση: Nα δείξετε ότι η εξίσωση παριστάνει μια έλλειψη με μεγάλο ημιάξονα α και εκκεντρότητα e.

Έλλειψη ονομάζεται ο γεωμετρικός τόπος των σημείων επιπέδου των οποίων το άθροισμα των αποστάσεων από δύο σταθερά σημεία, τις εστίες, είναι σταθερό και ισούται με 2α. Στην έλλειψη του παραπάνω σχήματος τα σημεία Α’ και Α παριστάνουν τις εστίες και ισχύουν: KB’=KB=α, ΓΑ=r, ΓΑ’=2α-r, A’A=2αe, όπου e=η εκκεντρότητά της. Φέρνουμε την ευθεία ΝΝ’ κάθετη στην εφαπτόμενη ΤΤ’. Η ΝΝ’ διχοτομεί την γωνία θ (γιατί;), οπότε φ+θ/2=90^ο ή θ=180^ο-2θ.

Δεδομένου ότι ΓΑ=r, ΓΑ’=2α-r, A’A=2αe, αν εφαρμόσουμε το νόμο των συνημιτόνων στο τρίγωνο (ΓΑ’Α) παίρνουμε: . Η σχέση αυτή μετά από μερικές πράξεις μας δίνει την ζητούμενη:

Συγκρίνοντας τις ‘πανομοιότυπες’ εξισώσεις (3) και (4) βλέπουμε ότι η τροχιά του πλανήτη είναι μια έλλειψη με μεγάλο ημιάξονα και εκεντρότητα .

Πηγή

Φανταστείτε έναν σουρεαλιστικό τρόπο σύνδεσης μιας ηλεκτρικής πηγής με έναν λαμπτήρα διαμέσου καλωδίων (μηδενικής αντίστασης) συνολικού μήκους 600.000 χιλιομέτρων, ενώ η πηγή και ο λαμπτήρας απέχουν μόνο 1 μέτρο!

Τίθεται το ερώτημα: μετά από πόσο χρόνο από το κλείσιμο του διακόπτη θα ανάψει ο λαμπτήρας;

• A) ~0,5 sec
• B) ~1 sec
• C) ~2 sec
• D) ~1/c sec (όπου c η ταχύτητα του φωτός σε m/s)
• E) κανένα από τα παραπάνω

Η απάντηση στο βίντεο που ακολουθεί:

Διαβάστε σχετικά: Energy transfer in electrical circuits: A qualitative account

… χρησιμοποιώντας ένα μπαλάκι, μια μετροταινία και ένα χρονόμετρο.

Αφήνουμε ένα μπαλάκι να πέσει ελεύθερα από ύψος . Αν  είναι το ύψος που φτάνει το μπαλάκι μετά την πρώτη αναπήδηση και  το χρονικό διάστημα  αναπηδήσεων, τότε να δείξετε ότι η επιτάχυνση της βαρύτητας υπολογίζεται από την σχέση:

όπου . (Υπόδειξη: )

Σύμφωνα με το παρακάτω βίντεο …

… αν κανείς βασιστεί στις αναπηδήσεις που κάνει το μπαλάκι του τένις (για το οποίο ισχύει λ≈0,5) θα μπορούσε να καταλήξει στην τιμή g=9,32 m/s² με ένα σφάλμα περίπου 17%. Αν χρησιμοποιούσε αργή κίνηση στο βίντεο θα μπορούσε να πάρει την τιμή g=9,80m/s² με σφάλμα περίπου 4%.

Και μια σχετική άσκηση που τέθηκε σε μαθητές Α’ Λυκείου την σχολική χρονιά 1972-73 (!): Ένα μπαλάκι αφήνεται να πέσει από ύψος 1,8 m. Μετά την πρώτη αναπήδηση ανεβαίνει σε ύψος 0,45 m. Θεωρήσατε ότι σε κάθε κρούση χάνει το ίδιο ποσοστό της μηχανικής του ενέργειας και ότι g=10 m/s² και υπολογίσατε σε πόσο χρόνο από την στιγμή της πρώτης κρούσης θα ακινητοποιηθεί.

διαβάστε την απάντηση ΕΔΩ.

Πηγή

Tα νετρόνια είναι ασταθή σωματίδια όταν βρίσκονται έξω από τον πυρήνα των ατόμων. Όταν ένα νετρόνιο διασπάται, μεταπίπτει σε πρωτόνιο εκπέμποντας ένα ηλεκτρόνιο και ένα αντι-νετρίνο:

Ο ακριβής προσδιορισμός του χρόνου ζωής των νετρονίων είναι μια από τις δυσκολότερες μετρήσεις στην πυρηνική φυσική.

Πριν από λίγες μέρες, η συνεργασία UCNτ από το εργαστήριο του Los Alamos δημοσίευσε την ακριβέστερη μέτρηση του χρόνου ζωής των νετρονίων που έγινε μέχρι σήμερα:

τ_n = 877,75 ± 0,36 s

Παραδόξως, δεν συγκρίνουν το αποτέλεσμα με προηγούμενες μετρήσεις, οπότε το έκανε αντ’ αυτών ο Martín González Alonso, δημοσιεύοντας το παρακάτω διάγραμμα στο Twitter:

Η γκρίζα ζώνη εκφράζει το εύρος του νέου μέσου όρου (878,64) που προκύπτει λαμβάνοντας υπόψιν όλες τις μετρήσεις και τα σφάλματά τους.

Tα μπλε σημεία προέρχονται από μετρήσεις με την ‘μέθοδο της φιάλης’, ενώ τα πράσινα από μετρήσεις με την ‘μέθοδο της δέσμης’. Οι πρώτη μετράει «ζωντανά νετρόνια», η δεύτερη «νεκρά».

Στην μέθοδο της φιάλης, υπερ-ψυχρά νετρόνια (UCN) με ενέργειες της τάξης των νανο-ηλεκτρονιοβόλτ, περιορίζονται σε μια παγίδα ή φιάλη που σχηματίζεται από συνδυασμούς μαγνητικών πεδίων, βαρύτητας και τοιχωμάτων. Ο χρόνος ζωής των νετρονίων προκύπτει μετρώντας τον αριθμό των σωματιδίων που επιβιώνουν στην παγίδα μετά από συγκεκριμένο χρονικό διάστημα. Με την μέθοδο της δέσμης, μια δέσμη νετρονίων γνωστής έντασης οδηγείται μέσα σε ηλεκτρομαγνητική παγίδα και μετρώνται τα πρωτόνια που προκύπτουν σε δεδομένο χρονικό διάστημα από την διάσπαση των νετρονίων.

Η ακριβής τιμή του χρόνου ζωής των νετρονίων παίζει σημαντικό ρόλο στην κοσμολογία και στην φυσική των στοιχειωδών σωματιδίων όπου καθορίζει παραμέτρους του Καθιερωμένου Προτύπου (στοιχείο Vud πίνακα Cabibbo–Kobayashi–Maskawaυ).

Πηγή