… ή ένα σωματίδιο μέσα σε μονοδιάστατο σωλήνα

Θεωρούμε ένα σωματίδιο μάζας m που βρίσκεται μέσα σε έναν πολύ λεπτό σωλήνα μήκους L, έτσι ώστε να κινείται χωρίς τριβές μόνο κατά την οριζόνται διεύθυνση του άξονα χ, σύφωνα με το παρακάτω σχήμα:

Τα άκρα του σωλήνα βρίσκονται στις θέσεις x=0 και x=L που είναι κλειστά και ακλόνητα. Η μόνη ενέργεια που μπορεί να έχει το σωματίδιο μέσα στον σωλήνα είναι η κινητική E=K=p²/2m – δεν υπάρχει δυναμική ενέργεια. Αν στο σωματίδιο δοθεί με κάποιο τρόπο οποιαδήποτε ταχύτητα, τότε αυτό θα κινείται ελεύθερα κατά μήκος του άξόνα χ, και θα ανακλάται ελαστικά προς την αντίθετη κατεύθυνση όταν θα φτάνει στα άκρα του σωλήνα.

Η συμπεριφορά του σωματιδίου σύμφωνα με την κλασική φυσική

Συνήθως το πρόβλημα αυτό αναφέρεται ως «σωματίδιο σε πηγάδι δυναμικού απείρου βάθους» δεδομένου ότι η δυναμική ενέργεια του σωματιδίου είναι  για 0<x<L και  για x<0, x>L (αφού θεωρούμε πως όταν το σωματίδιο χτυπάει στα άκρα του σωλήνα η ταχύτητά του αναστρέφεται ακαριαία, δηλ. αποκτά ‘άπειρη’ επιτάχυνση ή δέχεται ‘άπειρη’ δύναμη).

Τίθενται δύο ερωτήματα: (α) Μπορεί το σωματίδιο να κινηθεί με οποιαδήποτε κινητική ενέργεια; (β) όταν το σωματίδιο κινείται, ποιά είναι η πιθανότητα να βρεθεί σε κάποια περιοχή του άξονα χ;

Το πρώτο ερώτημα είναι προφανές.Το σωματίδιο μπορεί να παραμένει ακίνητο ή να του δώσουμε με κάποιο τρόπο την κατάλληλη ώθηση και να κινηθεί με οποιδήποτε κινητική ενέργεια.

Για το δεύτερο ερώτημα μπορούμε να πούμε τα εξής: Εφόσον τα άκρα του σωλήνα είναι ακλόνητα, τότε η πιθανότητα να βρεθεί έξω από αυτόν είναι μηδέν. Όσον αφορά τα σημεία στο εσωτερικό του σωλήνα (0<x<L) υποψιαζόμαστε ότι η πιθανότητα να βρεθεί οπουδήποτε στο εσωτερικό πρέπει να είναι η ίδια.

Ας συμβολίσουμε με ΔP(x) την πιθανότητα το σωματίδιο να βρεθεί σε μια στοιχειώδη απόσταση Δx στο εσωτερικό του σωλήνα, από την θέση x έως την x+Δx. Επειδή τα σημεία είναι άπειρα, βολεύει να εισάγουμε την έννοια της πυκνότητας πιθανότητας ρ(x)=ΔP(x)/Δx (πιθανότητα ανά μονάδα μήκους). Τότε, αφού το σωματίδιο πηγαινοέρχεται συνεχώς με την ίδια ταχύτητα (οι κρούσεις με τα τοιχώματα στα άκρα είναι ελαστικές) η πιθανότητα το σωματίδιο να βρίσκεται στο στοιχειώδες διάστημα Δx θα είναι ΔP(x)=Δx/L ή ρ(x)Δx=Δx/L, οπότε ρ(x)=1/L.

Συμπεραίνουμε λοιπόν σύμφωνα με την κλασική φυσική ότι: (α) το σωματίδιο μπορεί να έχει όποιαδήποτε ενέργεια από 0 έως το άπειρο και (β) η συνάρτηση πυκνότητας πιθανότητας να βρεθεί οπουδήποτε το σωματίδιο στο εσωτερικό του σωλήνα είναι ανεξάρτητη του x και ίση με 1/L. Όμως τι συμβαίνει στην πραγματικότητα; Αυτό θα μας το πει η κβαντική φυσική.

Η συμπεριφορά του σωματιδίου σύμφωνα με την κβαντική φυσική

Σύμφωνα με τον Louis de Broglie αφού τα ηλεκτρομαγνητικά κύματα (φως) μπορούν να συμπεριφέρονται ως σωματίδια (φωτόνια) όπως έδειξε το Einstein με την ερμηνεία του φωτοηλεκτρικού φαινομένου, τότε και τα σωματίδια θα μπορούσαν να συμπεριφέρονται ως κύματα. Αν η εξίσωση της ενέργειας ενός φωτονίου  συνδυαστεί με την εξίσωση ισοδυναμίας μάζας – ενέργειας  προκύπτει για το μήκος κύματος , όπου p=mc η ορμή του φωτονίου. Ο de Broglie επέκτεινε τη σχέση μήκους κύματος – ορμής και στα σωματίδια, θεωρώντας την κίνηση σωματιδίου ισοδύναμη με “κύμα” μήκους κύματος: . Πολλές φορές είναι βολική η έννοια του κυματαριθμού  που γράφεται ως , δεδομένου ότι .

Σύμφωνα λοιπόν με αυτή την πρωτόγονη κβαντική θεωρία το σωματίδιο (με κινητική ενέργεια Ε) στον μονοδιάστατο σωλήνα έχει κυματικές ιδιότητες και η συμπεριφορά του περιγράφεται από την κυματοσυνάρτηση . Η κυματοσυνάρτηση υψωμένη στο τετράγωνο εκφράζει την πυκνότητα πιθανότητας , την πιθανότητα ανά μονάδα μήκους να βρεθεί το σωματίδιο σε κάποια περιοχή του άξονα χ. Όμως το σωματίδιο είναι αδύνατον να βγεί από το απειρόβαθο πηγάδι και όπως στην κλασική φυσική, η πιθανότητα να βρεθεί έξω από το διάστημα 0<x<L είναι μηδενική. Το ίδιο θα ισχύει και στα όρια , επομένως στο εσωτερικό θα έχουμε ένα στάσιμο κύμα μήκους κύματος λ, με δεσμούς στα άκρα του.

Σύμφωνα με την γνωστή θεωρία των στάσιμων κυμάτων, θα πρέπει:  όπου . Όμως  και συνδιάζοντας τις δυο τελευταίες εξισώσεις προκύπτει ότι η ενέργεια του σωματιδίου μέσα στον σωλήνα θα είναι: , με .

Συμπεραίνουμε λοιπόν σύμφωνα με την κβαντική φυσική ότι (α) το σωματίδιο δεν μπορεί να έχει οποιαδήποτε τιμή στην κινητική του ενέργεια, αλλά συγκεκριμένες διακριτές τιμές και (β) Αφού η κυματοσυνάρτηση ως στάσιμο κύμα θα έχει την μορφή τριγωνομετρικής συνάρτησης, τότε η πυκνότητα πιθανότητας  να βρεθεί οπουδήποτε το σωματίδιο στο εσωτερικό του σωλήνα δεν θα είναι σταθερή.

Χρησιμοποιώντας την εξίσωση Schrödinger

Η κυματοσυνάρτηση υπακούει στην μονοδιάστατη (χρονοανεξάρτητη) εξίσωση του Schrödinger:  ή . Δεδομένου ότι , η εξίσωση γράφεται στην απλούστερη μορφή: . Εύκολα διαπιστώνεται ότι η  είναι λύση της εξίσωσης. Χρησιμοποιώντας τις οριακές συνθήκες , παίρνουμε ότι  και  ή , όπου . Αντικαθιστώντας το  στην , παίρνουμε ξανά την ενέργεια του σωματιδίου , ενώ η κυματοσυνάρτηση θα δίνεται από την εξίσωση: , όπου .

Διαμέσου μιάς νέας τεχνικής ανάλυσης, οι μετρήσεις ακριβείας της απόστασης Γης-Σελήνης θα βελτιώσουν τις εκτιμήσεις σχετικά με το υπόβαθρο των βαρυτικών κυμάτων στο σύμπαν.

Ο καταιγισμός όλων των βαρυτικών κυμάτων που βομβαρδίζουν συνεχώς την Γη στο εύρος συχνοτήτων της τάξης των νανο-Hertz (nHz – μία ταλάντωση ανά λίγες εβδομάδες περίπου) – μπορεί να ανιχνευθεί μετρώντας τις αναπαίσθητες επιδράσεις τους στο σύστημα Γης-Σελήνης. Υλοποιώντας αυτή την παλιά ιδέα οι φυσικοί έδειξαν ότι τα πιο πρόσφατα δεδομένα από λέιζερ θα μπορούσαν να χρησιμοποιηθούν για να τεθεί ένα αρκετά μικρότερο ανώτατο όριο στην πιθανή ένταση αυτών των κυμάτων, σε σύγκριση με προηγούμενες εκτιμήσεις. Η τεχνική αυτή υπόσχεται έναν νέο τρόπο ανίχνευσης βαρυτικών κυμάτων χρησιμοποιώντας φυσικά τροχιακά συστήματα ως ευαίσθητους ανιχνευτές.

Τα βαρυτικά κύματα μεταφέρουν πληροφορίες για μερικά από τα πιο βίαια γεγονότα στο σύμπαν, από τις συγχωνεύσεις μαύρων τρυπών έως και την Μεγάλη Έκρηξη, αλλά οι σημερινοί ανιχνευτές έχουν ένα τυφλό σημείο μεταξύ δύο διαφορετικών ζωνών συχνοτήτων. Η συνεργασία LIGO-Virgo-KAGRA—βασισμένη σε συμβολόμετρα λέιζερ που βρίσκονται στις ΗΠΑ, την Ευρώπη και την Ιαπωνία—μπορεί να ανιχνεύσει βαρυτικά κύματα με συχνότητες στην περιοχή από 1 έως 1000 Hz. Μια άλλη μέθοδος ανίχνευσης χρησιμοποιεί περιοδικά σήματα από πάλσαρ για την ανίχνευση βαρυτικών κυμάτων της τάξης μεγέθους των νανο-Hertz (1nHz=10^-9 Hz), που αντιστοιχεί σε μία ταλάντωση ανά λίγα χρόνια. Επομένως υπάρχει ένα μεγάλο κενό για τα βαρυτικά κύματα στην περιοχή συχνοτήτων μικρο-Hertz (1μHz=10^-6 Ηz), τα οποία θα μπορούσαν να προκύψουν, π.χ. από υπερμεγέθη δυαδικά ζεύγη μαύρων τρυπών στα τελευταία στάδια της περιφοράς τους πριν από την συγχώνευση.

«Σκοπεύουμε να καλύψουμε αυτό το κενό», υποστηρίζει ο Alexander Jenkins. «Η βασική ιδέα είναι να μετρήσουμε πώς [τα κύματα] επηρεάζουν τις τροχιές των δυαδικών συστημάτων, συμπεριλαμβανομένου και του συστήματος Γης-Σελήνης». Σύμφωνα με τον Jenkins πολλοί ερευνητές έχουν βοηθήσει στην ανάπτυξη αυτής της ιδέας από τη δεκαετία του 1970. Στην απλούστερη περίπτωση, ένα συνεχές βαρυτικό κύμα ίδιας συχνότητας με την τροχιακή κίνηση θα μπορούσε να ωθεί τα αντικείμενα λίγο πιο κοντά μεταξύ τους σε κάθε κύκλο. Εξαιτίας αυτού του φαινομένου συντονισμού, η τροχιά θα άλλαζε με την πάροδο του χρόνου με έναν τρόπο που εξαρτάται τις ιδιότητες του κύματος.

Το 2013, ο Lam Hui και οι συνεργάτες του έδειξαν ότι τα βαρυτικά κύματα στην περιοχή συχνοτήτων μHz θα μπορούσαν να έχουν δυνητικά μετρήσιμη επίδραση στα δυαδικά συστήματα. Απέδειξαν θεωρητικά ότι ένα συνεχές υπόβαθρο από μεγάλο αριθμό τέτοιων κυμάτων που προέρχονται από όλες τις κατευθύνσεις θα πρέπει να μεταβάλλει, σταδιακά με την πάροδο του χρόνου, την περίοδο και άλλες τροχιακές παραμέτρους. Και ο ρυθμός μεταβολής τους θα εξαρτάται από την ένταση των κυμάτων.

Χρησιμοποιώντας δεδομένα από ένα δυαδικό σύστημα άστρων τύπου πάλσαρ που εκπέμπει περιοδικά σήματα, ο Hui και οι συνεργάτες του υπολόγισαν ένα ανώτερο όριο στην πιθανή ισχύ των βαρυτικών κυμάτων στην περιοχή συχνοτήτων της τάξης μHz. Τώρα, οι Jenkins και Blas βελτίωσαν αυτή την εργασία, δείχνοντας ότι η ακρίβεια των τωρινών δεδομένων στο σύστημα Γης-Σελήνης επιτρέπει στους ερευνητές να εξαγάγουν ένα ανώτερο όριο που είναι πολύ μικρότερο από αυτό που προκύπτει από την εργασία των Hui et al.

Οι Jenkins και Blas βασίζονται σε παλαιότερες εργασίες για να αναπτύξουν έναν μαθηματικό φορμαλισμό, καθώς και αριθμητικές μεθόδους, για να παρακολουθήσουν την τυχαία εξέλιξη της τροχιακής κίνησης οποιουδήποτε δυαδικού συστήματος που υπόκειται σε ένα υπόβαθρο βαρυτικών κυμάτων. Αυτές οι μαθηματικές τεχνικές τους επέτρεψαν να κάνουν μια πιο ακριβή σύνδεση μεταξύ των τροχιακών μεταβολών και της φύσης των βαρυτικών κυμάτων που τις προκαλούν. «Ο φορμαλισμός μας δίνει έναν πολύ πιο ολοκληρωμένο και αυστηρό τρόπο υπολογισμού όλων των επιπτώσεων που θα είχε ένα υπόβαθρο βαρυτικών κυμάτων σε ένα δεδομένο δυαδικό σύστημα», λέει ο Jenkins.

Οι ερευνητές χρησιμοποιούν αυτές τις μεθόδους για να προτείνουν ένα τρόπο για την μείωση του ορίου όσον αφορά την ένταση του υποβάθρου των βαρυτικών κυμάτων στο τρέχον «τυφλό σημείο». Υποστηρίζουν ότι αυτό μπορεί να γίνει μέσα από την σύγκριση των μετρήσεων με λέιζερ της απόστασης Γης-Σελήνης με τις προβλέψεις της θεωρίας. Τα αποτελέσματα, σύμφωνα με τις εκτιμήσεις τους, θα πρέπει να βελτιώσουν τις γνώσεις των ερευνητών για το πιθανό πλάτος αυτών των κυμάτων περισσότερο από 100 φορές.

Σύμφωνα με τον Vitor Cardoso η ιδέα είναι απλή, αλλά απαιτεί δύσκολους υπολογισμούς για να εφαρμοστεί και να λειτουργήσει. Επιπλέον, αυτή η εναλλακτική προσέγγιση ανίχνευσης θα μπορούσε να αποκαλύψει απροσδόκητες πηγές βαρυτικών κυμάτων. Μπορεί να ανακαλύψουμε ότι το σύμπαν είναι γεμάτο από μυστηριώδη βαρυτικά κύματα.

Όσον αφορά τα επόμενα βήματα, ο Jenkins πιστεύει ότι χρειάζεται περισσότερη θεωρητική δουλειά. Για παράδειγμα, υποστηρίζει πως δεν πρέπει να περιοριστούμε στα μεμονωμένα δυαδικά συστήματα, αλλά πρέπει επίσης να δούμε πώς ανταποκρίνονται ολόκληροι γαλαξίες στα βαρυτικά κύματα.

Πηγή

Πριν από 100 χρόνια, τις πρώτες πρωινές ώρες της 8ης Φεβρουαρίου 1922, οι Stern και Gerlach διοχέτευσαν μια δέσμη ατόμων αργύρου σε ένα μαγνητικό πεδίο και παρατήρησαν τον διαχωρισμό της. Χωρίς να συνειδητοποιούν αρχικά τι έβλεπαν, οι Otto Stern και Walther Gerlach ανακάλυψαν το σπιν των ηλεκτρονίων.

Όπως θα εξηγούσε ο φυσικός Wolfgang Pauli το 1927, το σπιν είναι εντελώς διαφορετικό φυσικό μέγεθος σε σχέση με άλλα μεγέθη. Μπορεί να απεικονίζεται συχνά ως βέλος, αλλά είναι ένα βέλος που δεν ‘ζει’ στις τρεις διαστάσεις του χώρου. Αντίθετα, βρίσκεται σε μια τετραδιάστατη μαθηματική οντότητα που ονομάζεται χώρος Hilbert.

Το άτομο του αργύρου στην εξωτερική του στιβάδα (5s) διαθέτει ένα ηλεκτρόνιο και η μαγνητική ροπή των ατόμων του αργύρου οφείλεται αποκλειστικά στο σπιν αυτού του ηλεκτρονίου. Οι Stern και Gerlach παρατήρησαν ότι τα άτομα αργύρου στην δέσμη τους συμπεριφέρονταν σαν μικροσκοπικοί ραβδόμορφοι μαγνήτες αλληλεπιδρώντας με το μαγνητικό πεδίο. Όταν το μαγνητικό πεδίο ήταν απενεργοποιημένο, η δέσμη κινούνταν ευθύγραμμα σχηματίζοντας απλώς στην ίδια ευθεία μια αχνή κουκκίδα στην οθόνη. ‘Οταν ενεργοποιούσαν το μαγνητικό πεδίο η δέσμη διαχωρίζονταν σχηματίζοντας δυο κηλίδες πάνω και κάτω, συμμετρικά ως προς την προηγούμενη.

Στο βίντεο που ακολουθεί περιγράφεται σχηματικά το πείραμα Stern-Gerlach και μας δείχνει τι έπρεπε να συμβεί στην περίπτωση που το σπιν των ηλεκτρονίων τα έκανε να συμπεριφέρονται σαν κλασικοί ραβδόμορφοι μαγνήτες και πως συμπεριφέρονται στην πραγματικότητα αποδεικνύοντας ότι είναι κβαντικό μέγεθος:

Επιπλέον, το πείραμα μας δείχνει κι άλλη μια ιδιομορφία του σπιν των ηλεκτρονίων. Ότι η μαγνητική ροπή του σπιν είναι δυο φορές μεγαλύτερη σε σχέση με εκείνη της τροχιακής στροφορμής. Κι αυτό προκύπτει από το γεγονός ότι η απόσταση των κηλίδων στο πείραμα είναι διπλάσια από την αναμενόμενη.

Ο Stern αντιπαθούσε την κβαντική θεωρία και μαζί με τον φίλο του Max von Laue, είχαν δεσμευτεί ότι «αν αυτή η ανοησία του Bohr αποδειχτεί τελικά σωστή, θα εγκαταλείψουν τη φυσική». Τελικά ο Stern δεν εγκατέλειψε την φυσική, αλλά βραβεύθηκε με το Νόμπελ φυσικής το 1943, ενώ μαινόταν ο Β’ Παγκόσμιος Πόλεμος όχι για το πείραμα που έκανε με τον Gerlach αποκαλύπτοντας το σπιν των ηλεκτρονίων, αλλά για την ανακάλυψη της μαγνητικής ροπής του πρωτονίου.

Ο Stern είχε εγκαταλείψει από το 1933 την Γερμανία λόγω της εβραϊκής καταγωγής του. Ο Gerlach δεν κέρδισε ποτέ βραβείο Νόμπελ, ίσως λόγω της συμμετοχής του στην προσπάθεια του ναζιστικού καθεστώτος να κατασκευάσει πυρηνική βόμβα.

Διαβάστε περισσότερα στο άρθρο του Scientific American: ‘100 Years Ago, a Quantum Experiment Explained Why We Don’t Fall through Our Chairs‘

Πηγή

Μια προκλητική κβαντική υπόθεση αμφισβητεί την αντικειμενική πραγματικότητα

Η φίλη μου η Έμιλυ, μου λέει συχνά τα όνειρά της κι εγώ λιγότερο συχνά της λέω τα δικά μου, τα οποία συνήθως είναι πολύ θολά και ασύνδετα για να τα διηγηθώ. Προσπαθούμε να εξηγήσουμε τα όνειρά μας, να βρούμε νόημα σε αυτά. Τι αποκαλύπτουν για τους φόβους και τις επιθυμίες μας;

Η ερμηνεία των ονείρων είναι μια ατελής, άκρως υποκειμενική τέχνη, όπως σίγουρα θα ομολογούσε ο Sigmund Freud, στις σπάνιες στιγμές της ταπεινότητάς του. Τα όνειρα είναι εντελώς ιδιωτικές εμπειρίες ενός προσώπου, που δεν αφήνουν ίχνη πέρα ​​από την ελλιπή μνήμη του ονειροπόλου.

Κι όμως, το να δίνουμε νόημα στα όνειρα, δεν είναι εντελώς διαφορετικό από το να νοηματοδοτούμε την «πραγματικότητα», ότι κι αν είναι αυτή. Ναι, όλοι ζούμε στον ίδιο κόσμο. Μπορούμε να συγκρίνουμε σημειώσεις για το τι συμβαίνει και να βγάλουμε συμπεράσματα, με έναν τρόπο που δεν ισχύει για τα όνειρα.

Κι όμως η εμπειρία μας για τον κόσμο είναι μοναδική για τον καθένα μας. Το ίδιο και η ερμηνεία του, η οποία εξαρτάται από τις πεποιθήσεις μας, τις επιθυμίες, τις αποστροφές μας και ότι έχει σημασία για εμάς. Δεν είναι περίεργο που συχνά διαφωνούμε έντονα, και πολλές φορές βίαια, για το τι έχει συμβεί και τι σημαίνει.

Η επιστήμη προσφέρει την καλύτερη ελπίδα μας για την επίτευξη συναίνεσης σχετικά με το τι συμβαίνει. Οι επιστήμονες συγκεντρώνουν στοιχεία αποδεικτικών στοιχείων και προσπαθούν να συναρμολογήσουν αυτά τα θραύσματα σε μια συνεκτική ιστορία. Μετά από πολλές διαφωνίες και δεύτερες σκέψεις, οι επιστήμονες συγκλίνουν σε μια εύλογη αφήγηση. Οι σύγχρονοι άνθρωποι εξελίχθηκαν από πιθηκοειδή πλάσματα που ζούσαν στην Αφρική πριν από εκατομμύρια χρόνια. Ένας νέος, θανατηφόρος κορωνοϊός εμφανίστηκε στην Κίνα και εξαπλώνεται σε όλο τον κόσμο.

Όπως επισημαίνει ο φιλόσοφος Michael Strevens στο The Knowledge Machine, η επιστήμη επιλύει τις διαφορές μέσω επαναλαμβανόμενων παρατηρήσεων και πειραμάτων. Ο Strevens αποκαλεί την αφοσίωση των επιστημόνων στα εμπειρικά δεδομένα ως ο «σιδηρούς κανόνας της ερμηνείας». Στην ιδανική περίπτωση, ο σιδηρούς κανόνας παράγει ανθεκτικές, αντικειμενικά αληθινές θεωρήσεις του κόσμου.

Αλλά η υποκειμενικότητα είναι δύσκολο να εξαλειφθεί ακόμη και στη φυσική, το θεμέλιο πάνω στο οποίο στηρίζονται όλες οι επιστήμες. Η κβαντομηχανική, ένα μαθηματικό μοντέλο για την συμπεριφορά της ύλης στον μικρόκοσμο, είναι η πιο αυστηρά δοκιμασμένη θεωρία της επιστήμης. Αμέτρητα πειράματα την έχουν επιβεβαιώσει, όπως επίσης και τα τσιπ των υπολογιστών, τα λέιζερ και άλλες τεχνολογίες που εκμεταλλεύονται τα κβαντικά φαινόμενα.

Δυστυχώς, η κβαντική μηχανική αψηφά την κοινή λογική. Για περισσότερο από έναν αιώνα, μάταια οι φυσικοί προσπάθησαν να ερμηνεύσουν την θεωρία και να την μετατρέψουν σε μια ‘λογική’ ιστορία. «Κάθε επαρκής φυσικός μπορεί να ‘κάνει’ κβαντομηχανική», γράφει ο David J. Griffiths στο βιβλίο του ‘Introduction to Quantum Mechanics’, «αλλά οι ιστορίες που λέμε στους εαυτούς μας για αυτό που κάνουμε είναι τόσο διαφορετικές και σχεδόν τόσο απίθανες, όσο και τα παραμύθια της Σεχραζάντ».

Πολλοί φυσικοί αγνοούν τους γρίφους που θέτει η κβαντική μηχανική. Παίρνουν μια πρακτική, λειτουργική στάση απέναντι στη θεωρία, η οποία συνοψίζεται στην προτροπή, «Βούλωσέ το και υπολόγιζε!» Δηλαδή, ξεχάστε αυτά τα κβαντικά παράδοξα και συνεχίστε να εργάζεστε π.χ. για την κατασκευή του κβαντικού υπολογιστή, που μπορεί να σας κάνει πλούσιους!

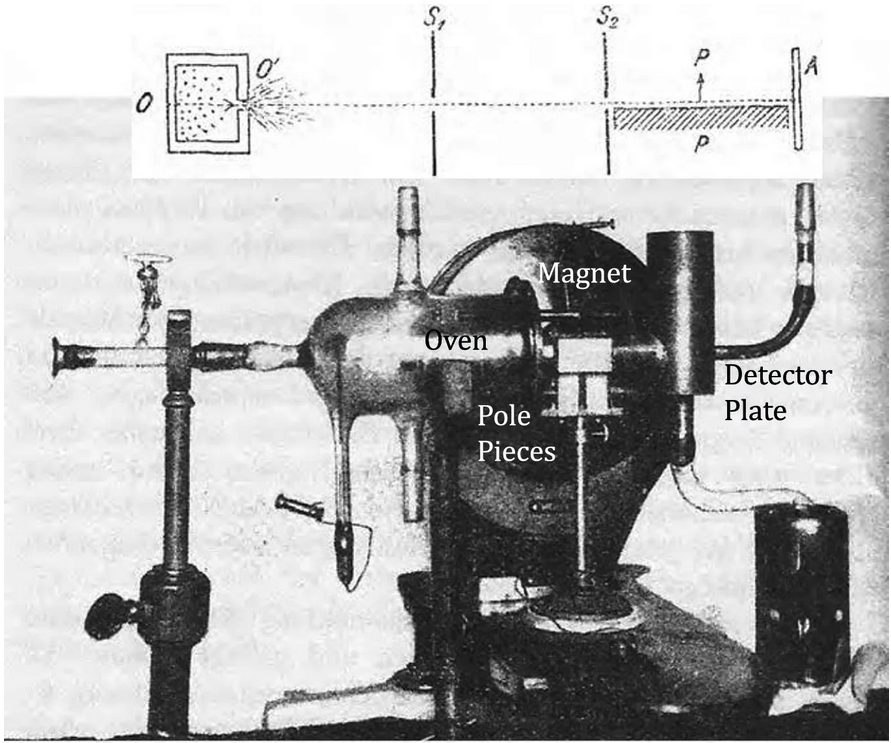
Άλλοι συνεχίζουν να διερευνούν τη θεωρία. Το 1961 ένας πρωτοπόρος θεωρητικός φυσικός, ο Eugene Wigner, πρότεινε ένα πείραμα σκέψης παρόμοιο με το αίνιγμα του γάτου του Schrödinger. Αντί για τον μυθικό γάτο σε ένα κουτί, φαντάστηκε ότι ένας φίλος του (ο φίλος του Wigner) βρίσκεται μέσα σε ένα εργαστήριο όπου υπάρχουν μια φιάλη που περιέχει θανατηφόρο αέριο, έναν απαριθμητή Geiger, και μια ραδιενεργή πηγή. Η ραδιενέργεια θα ενεργοποιούσε τον απαριθμητή Geiger, ο οποίος αναβοσβήνει, και στην συνέχεια θα έθετε σε κίνηση ένα σφυρί που θα έσπαγε το μπουκάλι και το δηλητηριώδες αέριο θα απελευθερωνόταν.

Τώρα φανταστείτε ότι ο Wigner είναι έξω από το εργαστήριο. Αν ο φίλος του Wigner δει τον ανιχνευτή να αναβοσβήνει, ξέρει ότι το θανατηφόρο αέριο θα απελευθερωθεί. Αλλά για τον Wigner, που βρίσκεται έξω από το εργαστήριο, η ραδιενεργή πηγή, ο φίλος του και ολόκληρο το εργαστήριο κυμαίνονται σε μια θολούρα πιθανών καταστάσεων. Ο Wigner και ο φίλος του φαίνεται να βρίσκονται σε δύο διαφορετικές πραγματικότητες.

Το 2020, οι φυσικοί πραγματοποίησαν μια εκδοχή του πειράματος σκέψης του Wigner και κατέληξαν στο συμπέρασμα ότι οι διαισθήσεις του ήταν σωστές. Σε μια είδηση ​​του Science με τίτλο “Quantum paradox points to shaky foundations of reality”, εικάζεται ότι το πείραμα θέτει υπό αμφισβήτηση την αντικειμενικότητα. «Θα μπορούσε να σημαίνει ότι δεν υπάρχει απόλυτο γεγονός», γράφει ο δημοσιογράφος George Musser, «κάτι που να είναι τόσο αληθινό για μένα όσο και για σένα».

Μια νέα ερμηνεία της κβαντικής μηχανικής που ονομάζεται QBism (προφέρεται «Κυβισμός», όπως το αντίστοιχο κίνημα της τέχνης) καθιστά την υποκειμενική εμπειρία το θεμέλιο της γνώσης και της ίδιας της πραγματικότητας. Ο David Mermin, ένας θεωρητικός φυσικός, λέει ότι η ερμηνεία QBism μπορεί να εξαφανίσει την «σύγχυση στα θεμέλια της κβαντικής μηχανικής». Απλώς πρέπει να αποδεχτείτε ότι όλη η γνώση ξεκινά με την «ατομική προσωπική εμπειρία».

Σύμφωνα με το QBism, ο καθένας από εμάς κατασκευάζει ένα σύνολο αντιλήψεων για τον κόσμο, με βάση τις αλληλεπιδράσεις του με αυτόν. Συνεχώς και σιωπηρά, ενημερώνουμε τις πεποιθήσεις μας όταν αλληλεπιδρούμε με συγγενείς που αρνούνται να εμβολιαστούν, με επιστήμονες που με 110 νεκρούς την ημέρα θεωρούν ότι όλα πάνε καλά ή με ανιχνευτές που εντοπίζουν φωτόνια. Η μεγάλη πραγματικότητα στην οποία ζούμε όλοι αναδύεται από τις συγκρούσεις όλων των υποκειμενικών μας μικρο-πραγματικοτήτων.

Οι QBists κρύβουν τον νου-κεντρισμό τους, έστω και μόνο για να μην θεωρούνται τρελλοί ή μυστικιστές. Αποδέχονται ότι η ύλη υπάρχει, όπως επίσης και ο νους, και απορρίπτουν τον σολιψισμό, ο οποίος υποστηρίζει ότι κανένα ον με αισθήσεις δεν μπορεί πραγματικά να είναι σίγουρο ότι αντιλαμβάνεται τον κόσμο με τον ίδιο τρόπο όπως κάποια άλλη παρόμοια ύπαρξη. Αλλά το βασικό μήνυμα του QBism, υπογραμμίζει η δημοσιογράφος Amanda Gefter, είναι η ιδέα ότι «μια ενιαία αντικειμενική πραγματικότητα είναι μια ψευδαίσθηση». Ένα όνειρο, θα μπορούσατε να πείτε.

Οι υποστηρικτές διαφωνούν για τους ορισμούς και οι φυσικοί και οι φιλόσοφοι που αγαπούν την αντικειμενικότητα απορρίπτουν πλήρως την ερμηνεία QBism. Όλη αυτή η διαμάχη, ειρωνικά, φαίνεται να επιβεβαιώνει την υπόθεση του QBism ότι δεν υπάρχει απόλυτη αντικειμενικότητα. υπάρχουν μόνο υποκειμενικές, οι προσωπικές απόψεις.

Οι φυσικοί έχουν περισσότερα κοινά από όσα θα ήθελαν να παραδεχτούν με τους καλλιτέχνες, οι οποίοι προσπαθούν να μετατρέψουν το χάος των πραγμάτων σε μια αφήγηση γεμάτη νόημα. Μερικοί καλλιτέχνες αποτρέπουν την επιθυμία μας για νόημα. Το ποίημα του T. S. Eliot «Η έρημη χώρα» είναι ένα συνονθύλευμα εικόνων που ξεπροβάλλουν μέσα και έξω από το κενό. Το ποίημα μοιάζει με όνειρο ή εφιάλτη. Το νόημά του είναι ότι δεν υπάρχει κανένα νόημα, δεν υπάρχει κύρια αφήγηση. Η ζωή είναι ένα αστείο και το αστείο είναι δικό σου αν πιστεύεις το αντίθετο.

Αν είστε πρακτικός άνθρωπος, όπως ένας πρωτοετής φοιτητής των οικονομικών επιστημών που παρακολουθεί το μάθημα λογοτεχνίας, μπορεί να συμπεράνετε όπως και ο T. S. Eliot, ότι οι προσπάθειες κατανόησης της ύπαρξης είναι μάταιες. Μπορεί να παροτρύνετε τους φίλους που ειδικεύονται στη φιλοσοφία να απολαύσουν τη ζωή αντί να ανησυχούν για το νόημά της. Μπορείτε να συνοψίσετε αυτή τη συμβουλή με ένα πιασάρικο σύνθημα: «Βουλώστε το και δημιουργήστε!» Αλλά ακόμη και αυτοί οι πραγματιστές πρέπει να αναρωτιούνται πότε πότε τι σημαίνει το κοινό μας όνειρο.

Τα παραπάνω είναι μια ελεύθερη και συνοπτική απόδοση ενός άρθρου του δημοσιογράφου John Horgan που δημοσιεύθηκε χθες στο περιοδικό scientificamerican. Αν σας δημιουργήθηκαν απορίες, υπάρχουν αρκετοι τρόποι για να τις απαντήσετε. Για παράδειγμα, μπορείτε να μελετήσετε τα βιβλία κβαντομηχανικής του Στέφανου Τραχανά, ο οποίος ως φυσικός αντί ‘να το βουλώσει κάνοντας υπολογισμούς’, επέλεξε να κατανοήσει και στη συνέχεια να εκλαϊκεύσει την κβαντομηχανική. Πρόσφατα μάλιστα κυκλοφόρησε το κατάλληλο για τέτοιους προβληματισμούς βιβλίο του: ‘Οι ερμηνείες της κβαντομηχανικής‘.

Πηγή

Θεωρούμε το παρακάτω κύκλωμα τεσσάρων αντιστατών (δυο με αντίσταση α και δυο με αντίσταση b):

H ολική αντίσταση θα είναι R=(α+b)/2. Στη συνέχεια συνδέουμε τα σημεία P και Q του κυκλώματος κλείνοντας τον διακόπτη. Παρατηρούμε ότι το αμπερόμετρο δείχνει πως το ηλεκτρικό ρεύμα αυξήθηκε. Αυτό σημαίνει πως η νέα ολική αντίσταση του κυκλώματος μειώθηκε(*): R’=2αb/(α+b)≤R=(α+b)/2 (στην περίπτωση που α=b η ολική αντίσταση παραμένει η ίδια).

Έχουμε λοιπόν ότι αb≤(α+b)²/4, δηλαδή … αποδείξαμε την γνωστή ανισότητα μεταξύ γεωμετρικού και αριθμητικού μέσου δύο θετικών αριθμών α και b:

Κι όχι μόνο. Από την R=(α+b)/2≥R’=2αb/(α+b) παίρνουμε: , δηλαδή την διπλή ανισότητα που εκτός από τον αριθμητικό και γεωμετρικό μέσο, περιλαμβάνει και τον αρμονικό μέσο των αριθμών α και b:

Mπορούμε να χρησιμοποιήσουμε την παραπάνω μέθοδο αποδεικνύοντας την γενικευμένη ανισότητα μεταξύ αριθμητικού και αρμονικού μέσου, θεωρώντας το παρακάτω κύκλωμα αντιστατών:

Όπως προηγουμένως διαπιστώνουμε πειραματικά ότι η ολική αντίσταση του κυκλώματος, όταν όλοι οι διακόπτες είναι ανοιχτοί, είναι μεγαλύτερη από την ολική αντίσταση όταν όλοι οι διακόπτες είναι κλειστοί, και έτσι εύκολα καταλήγουμε στην ανισότητα:

(*) Αποδεικνύεται και θεωρητικά πως όταν σ’ ένα κύκλωμα προκαλούμε βραχυκύκλωμα (μετατρέποντας κάποιες διαδρομές με άπειρη αντίσταση σε μηδενική αντίσταση), τότε η συνολική αντίσταση του κυκλώματος μειώνεται.

Πηγή

Η είδηση δεν είναι ότι το διαστημικό τηλεσκόπιο της ESA, Cheops, ανακάλυψε έναν ακόμα εξωπλανήτη, τον WASP-103b, αλλά το ότι ο εν λόγω εξωπλανήτης δεν είναι σφαιρικός και μοιάζει με μπάλα του ράγκμπι. Και είναι η πρώτη φορά που εντοπίζεται ένας τέτοιος παραμορφωμένος εξωπλανήτης.

O εξωπλανήτης WASP-103b ολοκληρώνει μια περιφορά γύρω από το άστρο του μέσα σε 24 ώρες και κινείται πολύ κοντά σ’ αυτό, διαγράφοντας τροχιά ακτίνας περίπου 0,02 αστρονομικές μονάδες. Γι αυτό οι αστρονόμοι περίμεναν ότι η τροχιά σε μια τόσο κοντινή απόσταση θα προκαλούσε ισχυρές παλιρροϊκές δυνάμεις, αλλά δεν ήταν σε θέση να τις μετρήσουν. Χρησιμοποιώντας τα νέα δεδομένα από το διαστημικό τηλεσκόπιο Cheops, σε συνδυασμό με δεδομένα που είχαν ήδη ληφθεί από τα διαστημικά τηλεσκόπια Hubble και Spitzer, κατάφεραν να διαπιστώσουν την παραμόρφωση εξαιτίας των παλιρροϊκών δυνάμεων του εξωπλανήτη WASP-103b στο σχήμα μιας μπάλας του ράγκμπι.

Οι παλίρροιες στην Γη οφείλονται στην βαρυτική αλληλεπίδραση της Γης με την Σελήνη που περιφέρεται γύρω μας. Κι ο Ήλιος έχει επίσης μια μικρή αλλά σημαντική επίδραση στις παλίρροιες, όμως είναι πολύ μακριά από τη Γη για να προκαλέσει μεγάλες παραμορφώσεις στον πλανήτη μας. Δεν μπορούμε να πούμε το ίδιο και για τον WASP-103b, που περιφέρεται πολύ κοντά στο άστρο του.

Η αντίσταση ενός υλικού στην παραμόρφωση εξαρτάται από τη σύνθεσή του. Για παράδειγμα, οι παλιρροϊκές δυνάμεις στην Γη λόγω Σελήνης και Ήλιου, προκαλούν την ‘υδατική παραμόρφωση’, δηλαδή τις παλίρροιες, αλλά δεν καταφέρνουν να παραμορφώσουν σημαντικά το βραχώδες τμήμα της.

Οι αστροφυσικοί συσχετίζουν την παλλιρροϊκή παραμόρφωση με τον αριθμό Love. Όσο μεγαλύτερος είναι ο αριθμός αυτός, τόσο πιο παραμορφωμένος είναι o πλανήτης. Ο αριθμός Love του WASP-103b είναι περίπου ίδιος με τον αντίστοιχο του του Δία, κι αυτό δείχνει ότι μάλλον έχουν παρόμοια εσωτερική δομή, παρά το γεγονός ότι ο WASP-103b έχει διπλάσια ακτίνα. Οι ερευνητές θα επιχειρήσουν την διερεύνηση των λεπτομερειών της εσωτερικής του δομής του με μελλοντικές παρατηρήσεις, ώστε να κατανοήσουν γιατί είναι τόσο παραμορφωμένος. Σημαντικό ρόλο στην ερμηνεία θα παίξει και ο προσδιορισμός του μεγέθους του πυρήνα του.

Δεδομένου ότι η αβεβαιότητα στην τιμή του αριθμού Love είναι προς το παρόν αρκετά μεγάλη, απαιτούνται επιπλέον παρατηρήσεις με τα διαστημικά τηλεσκόπια Cheops και James Webb. Η εξαιρετικά υψηλή ακρίβεια του Webb θα βελτιώσει τις μετρήσεις της παλιρροιακής παραμόρφωσης των εξωπλανητών, επιτρέποντας μια καλύτερη σύγκρισή τους με τους πλανήτες-γίγαντες του ηλιακού μας συστήματος.

Όμως υπάρχει άλλο ένα μυστήριο που περιβάλλει τον WASP-103b. Οι παλιρροϊκές αλληλεπιδράσεις μεταξύ άστρου και του συγκεκριμένου εξωπλανήτη έπρεπε να προκαλέσουν μείωση της τροχιακής περιόδου του και τη σταδιακή προσέγγιση στο άστρο του με τελικό αποτέλεσμα την σύγκρουσή του με αυτό. Όμως οι μετρήσεις του WASP-103b δείχνουν αντίθετα ότι η τροχιακή περίοδος ίσως να αυξάνεται και ότι ο εξωπλανήτης απομακρύνεται αργά από το άστρο του. Αυτό μπορεί να σημαίνει ότι κάτι διαφορετικό από τις παλιρροϊκές δυνάμεις είναι ο βασικός παράγοντας που επηρεάζει αυτόν τον εξωπλανήτη.

Έτσι, οι αστροφυσικοί εξέτασαν και άλλα πιθανά σενάρια. Θα μπορούσε για παράδειγμα, η δυναμική του συστήματος να επηρεάζεται από την παρουσία ενός δεύτερου άστρου ή η τροχιά του πλανήτη να είναι ελαφρώς ελλειπτική. Δεν μπόρεσαν να επιβεβαιώσουν αυτά τα σενάρια, αλλά ούτε και να τα αποκλείσουν. Για να απαντηθούν με βεβαιότητα όλα τα ερωτήματα θα απαιτηθούν επιπλέον παρατηρήσεις των διελεύσεων του WASP-103b (μπροστά από το άστρο του) από το Cheops και άλλα τηλεσκόπια.

Το σίγουρο είναι πως η ακρίβεια των παρατηρήσεων του διαστημικού τηλεσκοπίου Χέωψ (CHaracterising ExOPlanets Satellite), που έτυχε να είναι συνονόματο με έναν σκληρό και αδίστακτο Φαραώ, αποκάλυψε για πρώτη φορά το περίεργο σχήμα του WASP-103b, ανοίγοντας νέους δρόμους όσον αφορά την μελέτη εξωπλανητών.

Πηγή

Σε δημοσίευση στο περιοδικό Nature, οι φυσικοί της ερευνητικής ομάδας BASE στο CERN, περιγράφουν την ακριβέστερη σύγκριση, μέχρι τώρα, μεταξύ πρωτονίων και αντιπρωτονίων. Αναλύοντας τις μετρήσεις που πραγματοποιήθηκαν στο ‘εργοστάσιο’ αντιύλης του CERN, η ομάδα BASE μέτρησε το πηλίκο q/m (ηλεκτρικό φορτίο προς μάζα) των πρωτονίων (p) και των αντιπρωτονίων () με εκπληκτική ακρίβεια. Διαπίστωσαν ότι οι δύο λόγοι ταυτίζονται με μια πειραματική αβεβαιότητα 16 προς ένα τρισεκατομμύριο:

Σύμφωνα με το Καθιερωμένο Πρότυπο των στοιχειωδών σωματιδίων, τα σωματίδια ύλης και αντιύλης μπορεί να διαφέρουν, π.χ. στον τρόπο με τον οποίο μετατρέπονται σε άλλα σωματίδια, αλλά οι περισσότερες ιδιότητές τους, συμπεριλαμβανομένων και των μαζών τους, πρέπει να είναι πανομοιότυπες. Η εύρεση οποιασδήποτε μικρής διαφοράς μεταξύ των μαζών πρωτονίων και αντιπρωτονίων, ή μεταξύ των λόγων q/m, θα έσπαγε μια θεμελιώδη συμμετρία που ονομάζεται συμμετρία CPT και θα οδηγούσε σε νέα φυσική πέρα ​​από το Καθιερωμένο Πρότυπο. Μια τέτοια διαφορά θα μπορούσε επίσης να ρίξει φως στο γιατί το σύμπαν αποτελείται σχεδόν εξ ολοκλήρου από ύλη, παρόλο που κατά την Μέγάλη Έκρηξη προέκυψαν ίσες ποσότητες ύλης και αντιύλης. Όμως, οι διαφορές μεταξύ σωματιδίων ύλης και αντιύλης που προκύπτουν από τα πειράματα είναι τάξεις μεγέθους μικρότερες από τις τιμές που απαιτούνται για να κλονίσουν το Καθιερωμένο Πρότυπο.

Τα αρχικά CPT αναφέρονται, C: στην συζυγία φορτίου, τον μετασχηματισμό όπου ένα σωματίδιο αντικαθίσταται από το αντισωματίδιό του, P: στην ομοτιμία, η οποία συνδέεται με τον μετασχηματισμό αναστροφής του χώρου, και T: στη συμμετρία αναστροφής του χρόνου, όπου εναλλάσσονται οι χρονικές συντεταγμένες t και -t.
Oι ισχυρές και οι ηλεκτρομαγνητικές αλληλεπιδράσεις παραμένουν αναλλοίωτες κάτω από τους προαναφερθέντες μετασχηματισμούς C, P και T, ενώ οι ασθενείς αλληλεπιδράσεις παραβιάζουν μεμονωμένα και τις 3 αυτές συμμετρίες. Όμως, όταν οι μετασχηματισμοί C, P, Τ εφαρμόζονται μαζί, ως μετασχηματισμός CPT, τότε όλες οι αλληλεπιδράσεις – ασθενείς, ισχυρές και ηλεκτρομαγνητικές – παραμένουν αναλλοίωτες. Αυτό είναι το θεώρημα CPΤ και διατυπώνεται απλούστερα ως εξής: ένα σύστημα παραμένει αμετάβλητο αν τα σωματίδια αντικατασταθούν από τα κατοπτρικά συμμετρικά αντισωματίδιά τους και αντιστραφεί η ροή του χρόνου. To «αναλλοίωτο CPT» μας εγγυάται ότι ένα σωματίδιο και το αντισωματίδιό του έχουν ίσες μάζες, ίσους χρόνους ζωής, ίδιο σπιν, αλλά αντίθετους προσθετικούς κβαντικούς αριθμούς όπως το ηλεκτρικό φορτίο, η z συνιστώσα του ισοσπίν, ο κβαντικός αριθμός της παραξενιάς κ.ά.Όλα τα πειράματα που έχουν γίνει μέχρι σήμερα δείχνουν ότι δεν παραβιάζεται η συμμετρία CPT.

Για να πραγματοποιηθούν οι μετρήσεις πρωτονίων και αντιπρωτονίων, η ομάδα BASE εγκλώβισε τα αντιπρωτόνια και τα αρνητικά φορτισμένα ιόντα υδρογόνου (άτομα υδρογόνου στα οποία προστίθεται ένα επιπλέον ηλεκτρόνιο που χρησιμιμοποιώνται ως υποκατάστατα των πρωτονίων), σε μια συσκευή που ονομάζεται παγίδα Penning. Εκεί, ένα σωματίδιο ακολουθεί μια κυκλική τροχιά με συχνότητα, κοντά στη συχνότητα του κυκλότρου, η ακτίνα της οποίας εξαρτάται από την ένταση του μαγνητικού πεδίου και τον λόγο του ηλεκτρικού φορτίου προς την μάζα του σωματιδίου.

Διοχετεύοντας αντιπρωτόνια και αρνητικά φορτισμένα ιόντα υδρογόνου στην παγίδα, η ομάδα BASE συνέκρινε, κάτω από τις ίδιες συνθήκες, τον λόγο q/m (φορτίο προς μάζα) των πρωτονίων και των αντιπροτωνίων. Διαπίστωσαν ότι είναι ίσoι με ακρίβεια 16 προς 1000000000000! Αυτό το αποτέλεσμα είναι τέσσερις φορές ακριβέστερο σε σχέση με την αντίστοιχη προηγούμενη μέτρηση.

Εκτός από τη σύγκριση του λόγου q/m πρωτονίων και αντιπρωτονίων με πρωτοφανή ακρίβεια, η ομάδα BASE χρησιμοποίησε τις μετρήσεις της για να θέσει αυστηρά όρια σε θεωρίες πέρα ​​από το Καθιερωμένο Πρότυπο οι οποίες παραβιάζουν την συμμετρία CPT, καθώς και για να ελέγξει την ασθενή αρχή ισοδυναμίας. Σύμφωνα με αυτή την αρχή, διαφορετικά σώματα στο ίδιο βαρυτικό πεδίο υφίστανται την ίδια επιτάχυνση απουσία δυνάμεων τριβής. Το πείραμα BASE και οι μετρήσεις συχνότητας περιστροφής πρωτονίων και αντιπρωτονίων στο κύκλοτρο έγιναν στο βαρυτικό πεδίο στην επιφάνεια της Γης. Οποιαδήποτε διαφορά της βαρυτικής αλληλεπίδρασης των πρωτονίων με την αντίστοιχη βαρυτική αλληλεπεδρίση των αντιπρωτονίων θα οδηγούσε σε διαφορά μεταξύ των συχνοτήτων περιστροφής πρωτονίων και αντιπρωτονίων.

Oι φυσικοί του BASE δεν βρήκαν τέτοια διαφορά μέσα στα όρια του σφάλματος του πειράματος. Το σφάλμα αυτής της μέτρησης είναι συγκρίσιμο με το αντίστοιχο σφάλμα των πειραμάτων που μελετούν την απευθείας ελεύθερη πτώση των πρωτονίων στο πεδίο βαρύτητας της Γης.

Πηγή